
某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.
(1)写出每户每月用水量x(吨)与支付费用y(元)的函数关系;
(2)该地一家庭记录了去年12个月的月用水量(x∈N*)如下表:
| 月用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
| 频数 | 1 | 3 | 3 | 3 | 2 |
请你计算该家庭去年支付水费的月平均费用(精确到1元);
(3)今年干旱形势仍然严峻,该地政府号召市民节约用水,如果每个月水费不超过12元的家庭称为“节约用水家庭”,随机抽取了该地100户的月用水量作出如下统计表:
| 月用水量x(吨) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
据此估计该地“节约用水家庭”的比例.
科目:高中数学 来源: 题型:
函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=x-1,则不等式xf(x)>0在[-1,3]上的解集为( )
A.(1,3) B.(-1,1)
C.(-1,0)∪(1,3) D.(-1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=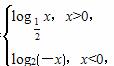 若f(m)<f(-m),则实数m的取值范围是( )
若f(m)<f(-m),则实数m的取值范围是( )
A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
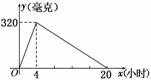 某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图像,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图像,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
A.上午10:00 B.中午12:00
C.下午4:00 D.下午6:00
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f′(n)的最小值是( )
A.-13 B.-15
C.10 D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com