练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝x3－x2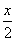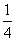＋＋.证明：存在x0∈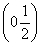，使f(x0)＝x0.


    证明：令g(x)＝f(x)－x.

    ∵g(0)＝，g＝f－＝

    －，∴g(0)·g<0.

    又函数g(x)在上连续，

    ∴存在x0∈，使g(x0)＝0，

    即f(x0)＝x0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在极坐标系中，从极点O作直线与另一直线相交于点M，在OM上取一点P，使．

    （1）求点P的轨迹方程；（2）设R为上任意一点，试求RP的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝20.2，b＝0.40.2，c＝0.40.6，则(　　)

    A．a>b>c                                            B．a>c>b

    C．c>a>b                                            D．b>c>a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝loga(1＋x)＋loga(3－x)(a>0，a≠1)，且f(1)＝2.

    (1)求a的值及f(x)的定义域．

    (2)求f(x)在区间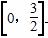上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


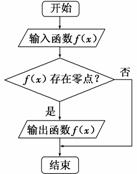
    执行如图所示的程序框图，若输入如下四个函数：

    ①y＝2x；　②y＝－2x；　③f(x)＝x＋x－1；④f(x)＝x－x－1.

    则输出函数的序号为(　　)

    A．①                                                 B．②

    C．③                                                 D．④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y与投放市场的月数x之间关系的是(　　)

    A．y＝100x　　　　　　                     B．y＝50x2－50x＋100

    C．y＝50×2x                                      D．y＝100log2x＋100

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地近年来持续干旱，为倡导节约用水，该地采用了“阶梯水价”计费方法，具体方法：每户每月用水量不超过4吨的每吨2元；超过4吨而不超过6吨的，超出4吨的部分每吨4元；超过6吨的，超出6吨的部分每吨6元．

    (1)写出每户每月用水量x(吨)与支付费用y(元)的函数关系；

    (2)该地一家庭记录了去年12个月的月用水量(x∈N*)如下表：

    月用水量x(吨)

    3

    4

    5

    6

    7

    频数

    1

    3

    3

    3

    2

    请你计算该家庭去年支付水费的月平均费用(精确到1元)；

    (3)今年干旱形势仍然严峻，该地政府号召市民节约用水，如果每个月水费不超过12元的家庭称为“节约用水家庭”，随机抽取了该地100户的月用水量作出如下统计表：

    月用水量x(吨)

    1

    2

    3

    4

    5

    6

    7

    频数

    10

    20

    16

    16

    15

    13

    10

    据此估计该地“节约用水家庭”的比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝(x－3)ex的单调递增区间是(　　)

    A．(－∞，2)                                      B．(0,3)

    C．(1,4)                                              D．(2，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知sin α<0，tan α>0.

    (1)求α角的集合；

    (2)求终边所在的象限；

    (3)试判断tansincos的符号．

    查看答案和解析>>

    同步练习册答案