Question

5．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点分别为F₁，F₂，O为双曲线的中心，P是双曲线右支上的点，△PF₁F₂的内切圆的圆心为I，且圆I与x轴相切于点A，过F₂作直线PI的垂线，垂足为B，若e为双曲线的离心率，则（　　）

• A． |OB|=|OA|
• B． |OA|=e|OB|
• C． |OB|=e|OA|
• D． |OB|与|OA|大小关系不确定

Answer 1

分析 根据题意，利用切线长定理，再利用双曲线的定义，把|PF₁|-|PF₂|=2a，转化为|AF₁|-|AF₂|=2a，从而求得点H的横坐标．再在三角形PCF₂中，由题意得，它是一个等腰三角形，从而在三角形F₁CF₂中，利用中位线定理得出OB，从而解决问题．

解答 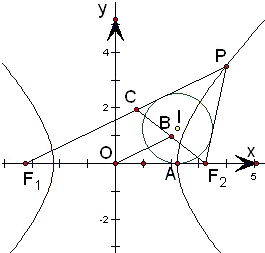解：F₁（-c，0）、F₂（c，0），内切圆与x轴的切点是点A
∵|PF₁|-|PF₂|=2a，及圆的切线长定理知，
|AF₁|-|AF₂|=2a，设内切圆的圆心横坐标为x，
则|（x+c）-（c-x）|=2a
∴x=a；
|OA|=a，
在△PCF₂中，由题意得，F₂B⊥PI于B，延长交F₁F₂于点C，利用△PCB≌△PF₂B，可知PC=PF₂，
∴在三角形F₁CF₂中，有：
OB=$\frac{1}{2}$CF₁=$\frac{1}{2}$（PF₁-PC）=$\frac{1}{2}$（PF₁-PF₂）=$\frac{1}{2}$×2a=a．
∴|OB|=|OA|．
故选：A．

点评 本题考查双曲线的定义、切线长定理．解答的关键是充分利用平面几何的性质，如三角形内心的性质等．