
| A. | 3 | B. | $\frac{10}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{27}$ |
分析 根据函数为偶函数得到,f(x)为周期为2的函数,继而得到f(log${\;}_{\frac{1}{3}}$10)=f(log3$\frac{10}{9}$),代值计算即可.
解答 解:由题意定义在R上的偶函数f(x),满足f(x+2)=f(-x),
∴f(x+2)=f(x),
∴f(x)为周期为2的函数,
∴f(log${\;}_{\frac{1}{3}}$10)=f(log310)=f(log310-2)=f(log3$\frac{10}{9}$)=${3}^{lo{g}_{3}\frac{10}{9}-1}$=$\frac{10}{9}÷3$=$\frac{10}{27}$,
故选:D.
点评 本题考点抽象函数的应用,函数的值求法,利用函数的性质通过转化来求函数的值,是函数性质综合运用的一道好题.对于本题中恒等式的意义要好好挖掘,做题时要尽可能的从这样的等式中挖掘出信息.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
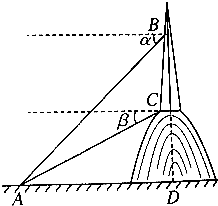 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).
在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-3<x<2} | D. | {x|-3<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
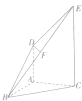 如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,
如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A、B、D三点共线 | B. | A、B、C三点共线 | C. | B、C、D三点共线 | D. | A、C、D三点共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$i | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$i | D. | -$\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com