
分析 (1)由直线l的极坐标方程为ρcosθ-$\sqrt{3}$ρsinθ=5,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$化为直角坐标方程,由圆C的参数方程为$\left\{\begin{array}{l}{x=5+2cosα}\\{y=4+2sinα}\end{array}\right.$(α为参数,α∈[0,2π]),利用sin2α+cos2α=1化为直角坐标方程.
(2)解法一:设圆心C到直线l的距离为d,利用点到直线的距离公式求出d,再与圆C的半径r=2,比较即可得出.
解法二:假设圆C与直线有公共点P(x,y),则$x-\sqrt{3}y-5=0$,将圆C的参数方程代入直线方程,有:$(5+2cosα)-\sqrt{3}(4+2sinα)=5$,判断是否有解即可.
解答 解:(1)由直线l的极坐标方程为ρcosθ-$\sqrt{3}$ρsinθ=5,化为直角坐标方程为:$x-\sqrt{3}y-5=0$,
由圆C的参数方程为$\left\{\begin{array}{l}{x=5+2cosα}\\{y=4+2sinα}\end{array}\right.$(α为参数,α∈[0,2π])化为直角坐标方程为:(x-5)2+(y-4)2=4.
(2)直线l与圆C相离.
解法一:设圆心C到直线l的距离为d,则$d=\frac{{|{5-\sqrt{3}×4-5}|}}{{\sqrt{{1^2}+{{(-\sqrt{3})}^2}}}}=2\sqrt{3}$,
∵圆C的半径r=2,∴d>r.
∴直线l与圆C相离.
解法二:假设圆C与直线有公共点P(x,y),
则有$x-\sqrt{3}y-5=0$和$\left\{\begin{array}{l}x=5+2cosα\\ y=4+2sinα\end{array}\right.({α为参数,α∈[0,2π)})$,
将圆C的参数方程代入直线方程,有:$(5+2cosα)-\sqrt{3}(4+2sinα)=5$,
整理得:$cosα-\sqrt{3}sinα=2\sqrt{3}$$2cos(α+\frac{π}{3})=2\sqrt{3}$$cos(α+\frac{π}{3})=\sqrt{3}>1$,此方程无解,
因此假设不成立,直线与圆相离.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-1,-$\frac{1}{3}$] | C. | (-∞,-1)∪[-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
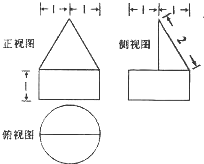
| A. | $\frac{\sqrt{3}π}{6}$+1 | B. | $\frac{\sqrt{3}π}{6}$+π | C. | $\frac{\sqrt{3}π}{3}$+π | D. | $\frac{\sqrt{3}π}{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com