
分析 (Ⅰ)运用离心率公式和最大值a+c,解方程即可得到a,c,求出b,进而得到椭圆方程;
(Ⅱ)求出A,B坐标,考虑MN斜率不存在,可得M,N坐标,求出直线AN,BN方程,求出交点,猜想:存在l:x=-8,再由分析法证明,设MN的方程是y=k(x+2),代入椭圆C的方程,运用韦达定理,即可得到存在定直线l:x=-8,使得AM与BN的交点Q总在直线l上.
解答 解:(Ⅰ)由$e=\frac{{\sqrt{3}}}{2}⇒\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,
又椭圆C上的点到焦点的距离的最大值$a+c=4+2\sqrt{3}$.
∴a=4,c=2$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{16-12}$=2,
所以椭圆C方程是:$\frac{x^2}{16}+\frac{y^2}{4}=1$;
(Ⅱ)证明:A(-4,0).B(4,0),
当MN斜率不存在时,MN:x=-2,$M(-2,\sqrt{3}),N(-2,-\sqrt{3})$,
则AN的方程是:y=$\frac{\sqrt{3}}{2}$(x+4),
BN的方程是:y=$\frac{\sqrt{3}}{6}$(x-4),
交点的坐标是:$(-8,-2\sqrt{3})$,猜想:存在l:x=-8,
即直线l的方程是:x=-8使得AM与BN的交点Q总在直线l上.
当MN斜率存在时,设MN的方程是y=k(x+2),代入椭圆C的方程得:
(1+4k2)x2+16k2x+16k2-16=0,
设M(x1,y1),N(x2,y2),Q(-8,y0)
∴${x_1}+{x_2}=\frac{{-16{k^2}}}{{1+4{k^2}}},{x_1}{x_2}=\frac{{16{k^2}-16}}{{1+4{k^2}}}$,
∵$\overrightarrow{AQ}=(-4,{y_0})$,$\overrightarrow{AM}$=(x1+4,y1),A,M,Q共线,
∴-4y1=y0(x1+4),
由x1+4≠0,可得y0=-$\frac{4{y}_{1}}{{x}_{1}+4}$,
又$\overrightarrow{BQ}=(-12,{y_0})$,$\overrightarrow{BN}=({x_2}-4,{y_2})$,
要证B,N,Q共线,即证$-12{y_2}=({x_2}-4)\frac{{-4{y_1}}}{{{x_1}+4}}$,
即证:3k(x2+2)(x1+4)=k(x1+2)(x2-4),
即证:x1x2+5(x1+x2)+16=0
因为:${x_1}{x_2}+5({x_1}+{x_2})+16=\frac{{16{k^2}-16}}{{1+4{k^2}}}-\frac{{80{k^2}}}{{1+4{k^2}}}+16=0$成立,
所以点Q在直线BN上.
综上:AM与BN的交点Q总在定直线l:x=-8上.
点评 本题考查椭圆方程求法,注意运用离心率公式和椭圆上点与焦点的最大值a+c,考查定直线问题的证明,注意运用猜想和分析法,考查化简整理的运算能力,属于中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{7}{10}$ | C. | $\frac{24}{35}$ | D. | $\frac{47}{70}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
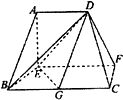 在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.
在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
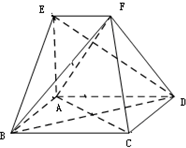 在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com