
 如图直三棱柱ABC-A1B1C1 中AC=2AA1,AC⊥BC,D、E 分别为A1C1、AB 的中点.求证:
如图直三棱柱ABC-A1B1C1 中AC=2AA1,AC⊥BC,D、E 分别为A1C1、AB 的中点.求证:分析 (1)只需证明BC⊥AD,DC⊥AD,证明 即可AD⊥平面BCD
(2)取BC中点O,连结DO、OE可得四边形A1DOE为平行四边形,即A1E∥OD,A1E∥平面BCD.
解答 证明:(1)∵直三棱柱ABC-A1B1C1中CC1⊥平面ABC,又BC?平面ABC,
∴CC1⊥BC,
又∵AC⊥BC,AC∩CC1=C,AC,CC1?平面AA1C1C,
∴BC⊥平面AA1C1C,
而AD?平面AA1C1C∴BC⊥AD…①
又该直三棱柱中AA1⊥A1C1,CC1⊥A1C1,
由已知AA1=$\frac{1}{2}$ AC=A1D,则∠A1DA=$\frac{π}{4}$,
同理∠C1DC=$\frac{π}{4}$,则∠ADC=$\frac{π}{2}$,即CD⊥AD,
由①BC⊥AD,BC∩CD=C,BC,CD?平面BCD,
∴AD⊥平面BCD;
(2)取BC中点O,连结DO、OE,∵AE=EB,CO=BO∴OE平行等于$\frac{1}{2}$ AC,
而A1D平行等于$\frac{1}{2}$AC,
∴A1D平行等于OE∴四边形A1DOE为平行四边形,
∴A1E∥OD,而A1E?平面BCD,OD?平面BCD,
∴A1E∥平面BCD.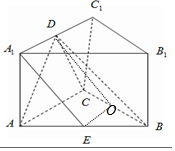
点评 本题考查了空间线面垂直、线面平行的判定,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{16}$-y2=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1 | D. | x2-$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)与g(x)的定义域为[m,n],它们的图象如图所示,则不等式f(x)g(x)<0的解集是{x|x∈(m,a)∪(a,b)∪(c,d)}.
函数f(x)与g(x)的定义域为[m,n],它们的图象如图所示,则不等式f(x)g(x)<0的解集是{x|x∈(m,a)∪(a,b)∪(c,d)}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (1,2) | C. | (1,+∞) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD与BDEF均为边长为2的菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为边长为2的菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e]∪[e,+∞﹚ | B. | [-e,e] | ||
| C. | ﹙-∞,-2-$\frac{1}{e}$]∪[-2+$\frac{1}{e}$,+∞﹚ | D. | [-2-$\frac{1}{e}$,-2+$\frac{1}{e}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.36 | B. | 0.64 | C. | 0.74 | D. | 0.63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com