
��A(xA,yA)��B(xB,yB)Ϊƽ��ֱ������ϵ�ϵ�����,����xA,yA,xB,yBÎZ.���x=xB-xA����y=yB-yA,��|��x|+|��y|=3����|��x|��|��y|��0,��Ƶ�BΪ��A�ġ���ص㡱,������B=f(A).
(1)����:��(0,0)�ġ���ص㡱�м���?�ж���Щ���Ƿ���ͬһ��Բ��,����,д��Բ�ķ��̣������ڣ�˵�����ɣ�
(2)��֪��H(9,3),L(5,3),����M����M=f(H),L=f(M),���M�����ꣻ
(3)��֪P0(x0,y0)(x0ÎZ,y0ÎZ)Ϊһ������, ����Pi����Pi=f (Pi-1),����i=1,2,3,������,n����|P0Pn|����Сֵ��
��1��x²+y²=5
��2��M(7,2)��M(7,4).
��3���� ʱ, |P0Pn|����СֵΪ
ʱ, |P0Pn|����СֵΪ ;
;
��n=2k,kÎN *ʱ, |P0Pn|����СֵΪ0��
��n=2k+1,kÎN *ʱ, |P0Pn|����СֵΪ1.
���������������: (1)��Ϊ|��x|+|��y|=3(|��x|,|��y|Ϊ��������),
��|��x|=1,|��y|=2��|��x|=2,|��y|=1,���Ե�(0,0)�ġ���ص㡱��8�� .
����Ϊ(��x)²+(��y)²=5,��(��x-0)²+(��y-0)²="5" .
������Щ����ֵ��Ӧ�ĵ�����(0,0)ΪԲ��, Ϊ�뾶��Բ�ϣ�
Ϊ�뾶��Բ�ϣ�
����Ϊx²+y²="5" . 3��
(2)��M(xM,yM),
��ΪM=f(H),L=f(M),
������|xM-9|+|yM-3|="3," |xM-5|+|yM-3|=3,
����|xM-9|=|xM-5|,����xM=7, yM=2��yM=4,
����M(7,2)��M(7,4). 6��
(3) ��n=1ʱ,��֪|P0Pn|����СֵΪ ;
;
��n=2k,kÎN *ʱ, |P0Pn|����СֵΪ0 ;
��n=3ʱ,���ڵ�P,��������ķ���ѡ����ص㡱,�ɵ�P3(x0,y0+1):
P0(x0,y0)��P1(x0+2,y0+1)��P2(x0+1,y0+3) ��P3(x0,y0+1)
��|P0Pn|����СֵΪ1,
��n=2k+3, kÎN *ʱ,���ڵ�P,����2k�α任�ص���ʼ��P0(x0,y0),Ȼ��3�α任�ص�Pn(x0,y0+1),��|P0Pn|����СֵΪ1.
����,�� ʱ, |P0Pn|����СֵΪ
ʱ, |P0Pn|����СֵΪ ;
;
��n=2k,kÎN *ʱ, |P0Pn|����СֵΪ0��
��n=2k+1,kÎN *ʱ, |P0Pn|����СֵΪ1. 10��
���㣺Բ�ķ��̣��������
��������Ҫ�ǿ�����Բ�ķ��̵���⣬�Լ�����������ֵ�������е��⡣



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪��L������ ����ֱ��L��x���ϵĽؾ������y���ϵĽؾ��2������ֱ��L�ķ���.
����ֱ��L��x���ϵĽؾ������y���ϵĽؾ��2������ֱ��L�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪Բ����C�� ����
���� �ֱ�ΪԲ����C�����ҽ��㣬��BΪԲ����C���϶��㣬����
�ֱ�ΪԲ����C�����ҽ��㣬��BΪԲ����C���϶��㣬���� �Ҵ�ֱ��ֱ��
�Ҵ�ֱ��ֱ�� ��ֱ��
��ֱ�� �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪�� �ķ���Ϊ3x��4y��12��0������������������ֱ��
�ķ���Ϊ3x��4y��12��0������������������ֱ��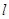 �ķ��̣�
�ķ��̣�
(1) 
 ����ֱ��
����ֱ��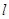 ����(��1,3)��
����(��1,3)��
(2) 
 ����
����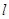 ����������Χ�ɵ����������Ϊ4.
����������Χ�ɵ����������Ϊ4.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪�� ������
������ ,���
,��� ��
��
��1��д��ֱ�� �IJ�������
�IJ�������
��2���� ��Բ
��Բ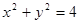 �ཻ������
�ཻ������ �����
����� ��
�� ����ľ���֮��
����ľ���֮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ƽ���ı��ε����ڱ�����ֱ�ߵķ���Ϊx��y��1��0��3x��4��0����Խ��ߵĽ�����D(3,3)�������������ڵ�ֱ�ߵķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ֱ��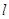 ����ֱ��
����ֱ�� ��
�� �صõ��߶��е�ΪP
�صõ��߶��е�ΪP
��1����ֱ��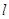 �ķ���
�ķ���
��2����֪�� ����ֱ��
����ֱ��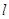 ����һ��M,ʹ
����һ��M,ʹ ��С������������Сֵ
��С������������Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����������15�֣�
��֪��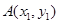 ��
�� ��������
�������� ���������㣬������
���������㣬������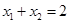 ��
��
������ ���д��߾�����
���д��߾����� ����ֱ��
����ֱ�� �ķ��̣�
�ķ��̣�
������ ���д��߽�
���д��߽� ���ڵ�
���ڵ� ����
���� ����������ֵ����ʱֱ��
����������ֵ����ʱֱ�� �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
(��������14��)��
����б����ֱ��y���� x��1����б�ǵ�
x��1����б�ǵ�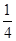 ���ҷֱ���������������ֱ�߷��̣�
���ҷֱ���������������ֱ�߷��̣�
(1)������( ����1)��
����1)��
(2)��y���ϵĽؾ��ǣ�5.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com