
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,判断函数的单调区间即可;
(Ⅱ)得到$g(x)=g({\frac{1}{x}})$,设$φ(x)=lng(x)=(x+\frac{1}{x})ln(1+x)-xlnx$,求出函数的导数,再二次求导,求出φ(x)的最大值,从而求出g(x)的最大值即可.
解答 解:(Ⅰ) 由题意知:函数f(x)的定义域为(-1,+∞),
且$f'(x)=\frac{1}{1+x}-\frac{{(2ax+1)(1+x)-2(a{x^2}+x)}}{{{{(1+x)}^3}}}=\frac{x(x-2a+3)}{{{{(1+x)}^3}}}$,
①当2a-3≤-1时,即a≤1时,
若x>0,则f'(x)>0;若-1<x<0,则f'(x)<0,
此时f(x)在区间(0,+∞)上单调递增,在区间 (-1,0)上单调递减.
②当-1<2a-3<0,即$1<a<\frac{3}{2}$时
若-1<x<2a-3或x>0,则f'(x)>0; 若2a-3<x<0,则f'(x)<0,
此时f(x)在区间(-1,2a-3),(0,+∞)上单调递增,在区间(2a-3,0)上单调递减.
③当2a-3=0时$a=\frac{3}{2}$时,f'(x)≥0,故此时f(x)在区间(-1,+∞)上单调递增.
④当2a-3>0时,即$\frac{3}{2}<a≤2$时
若-1<x<0或x>2a-3,则f'(x)>0,若0<x<2a-3,则f'(x)<0,
∴f(x)在区间(-1,0),(2a-3,+∞)上单调递增,在区间上(0,2a-3)单调递减.
(Ⅱ)显然$g(x)=g({\frac{1}{x}})$,设$φ(x)=lng(x)=(x+\frac{1}{x})ln(1+x)-xlnx$,
则$φ(x)=φ(\frac{1}{x})$,因此φ(x)在(0,+∞)上的最大值等于其在(0,1]上的最大值;
$φ'(x)=(1-\frac{1}{x^2})ln(1+x)+(x+\frac{1}{x})•\frac{1}{1+x}-lnx-1$,
设$h(x)=(1-\frac{1}{x^2})ln(1+x)+(x+\frac{1}{x})•\frac{1}{1+x}-lnx-1$,
$h'(x)=\frac{{2{{(1+x)}^2}[ln(1+x)-\frac{{2{x^2}+x}}{{{{(1+x)}^2}}}]}}{{{x^3}{{(1+x)}^2}}}$,
由(Ⅰ)知,当a=2时,f(x)在区间(0,1]单调递减,
所以$f(x)=ln(1+x)-\frac{{2{x^2}+x}}{{{{(1+x)}^2}}}<f(0)=0$,h'(x)<0,
所以函数h(x)在区间(0,1]单调递减,于是h(x)≥h(1)=0,
从而函数φ(x)在区间(0,1]单调递增,进而φ(x)≤φ(1)=2ln2,
因为φ(x)=lng(x),
所以函数g(x)的最大值等于4.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正视图是圆心角为270°的扇形,俯视图与侧视图中圆的半径为2,则这个几何体的表面积是( )
一个几何体的三视图如图所示,其中正视图是圆心角为270°的扇形,俯视图与侧视图中圆的半径为2,则这个几何体的表面积是( )| A. | 16π | B. | 14π | C. | 12π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
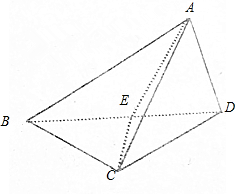 如图,在四面体ABCD中,CB=CD,AD⊥平面BCD,且E是BD的中点,求证:
如图,在四面体ABCD中,CB=CD,AD⊥平面BCD,且E是BD的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 交换律 | B. | 结合律 | ||
| C. | 交换律、结合律都不满足 | D. | 交换律、结合律都满足 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了调查某地区成年人血液的一项指标,现随机抽取了成年男性、女性各10人组成的一个样本,对他们的这项血液指标进行了检测,得到了如下茎叶图.根据医学知识,我们认为此项指标大于40为偏高,反之即为正常.
为了调查某地区成年人血液的一项指标,现随机抽取了成年男性、女性各10人组成的一个样本,对他们的这项血液指标进行了检测,得到了如下茎叶图.根据医学知识,我们认为此项指标大于40为偏高,反之即为正常.| 正常 | 偏高 | 合计 | |
| 男性 | |||
| 女性 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-8,-4+2$\sqrt{5}$) | B. | (-4-2$\sqrt{5}$,-4+2$\sqrt{5}$) | C. | (-4+2$\sqrt{5}$,8] | D. | (-4-2$\sqrt{5}$,-8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com