
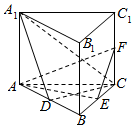
 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.分析 (1)由直棱柱可得BB1⊥平面ABC,得出BB1⊥AE,由等边三角形性质可得AE⊥BC,故而AE⊥平面BCC1B1,于是平面AEF⊥平面B1BCC1;
(2)由(1)的证明同理可得CD⊥平面ABB1A1,故而CD⊥A1D,∴A1D=CD,利用勾股定理求出AA1从而得出棱锥的高CF,代入棱锥的体积公式计算即可.
解答 (1)证明:∵B1B⊥平面ABC,AE?平面ABC,
∴B1B⊥AE,
∵△ABC是等边三角形,E是BC的中点,
∴AE⊥BC,又BC?平面BCC1B1,B1B?平面BCC1B1,B1B∩BC=B,
∴AE⊥平面BCC1B1,又AE?平面AEF,
∴平面AEF⊥平面B1BCC1.
(2)由(1)可知CD⊥平面ABB1A1,A1D?平面ABB1A1,
∴CD⊥A1D,
∵AB=AC=BC=2,D是AB的中点,E是BC的中点,
∴AE=CD=$\sqrt{3}$,AD=CE=1,
∵∠CA1D=45°,∴A1D=CD=$\sqrt{3}$,
∴AA1=$\sqrt{{A}_{1}{D}^{2}-A{D}^{2}}=\sqrt{2}$,
∵F是C1C的中点,
∴FC=$\frac{1}{2}{C}_{1}C=\frac{1}{2}{A}_{1}A=\frac{\sqrt{2}}{2}$.
∴VF-ACE=$\frac{1}{3}{S}_{△ACE}•FC$=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×1×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{12}$.
点评 本题考查了正三棱柱的结构特征,面面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | ($\overrightarrow{a}•\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}•\overrightarrow{c}$) | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
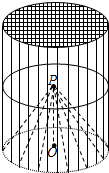 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
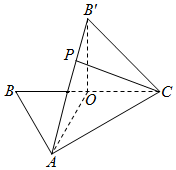 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(2x+$\frac{2π}{3}$) | C. | f(x)=2sin(x+$\frac{π}{3}$) | D. | f(x)=2sin(2x+$\frac{5π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com