
分析 (1)由$\overrightarrow b=(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,可得|b|=1,又|$\overrightarrow{a}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°可求得$\vec a•\vec b=-1$,从而可求得|$\overrightarrow{a}$+2$\overrightarrow{b}$|;
(2)由(a+kb)⊥(2b-a),得($\overrightarrow{a}$+k$\overrightarrow{b}$)•(2$\overrightarrow{b}$-$\overrightarrow{a}$)=0,可解得k=2.
解答 解:(1)因为$\overrightarrow b=(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,所以|b|=1,
又|$\overrightarrow{a}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°
∴$\vec a•\vec b=-1$.…(3分)
$|\overrightarrow{a}+2\overrightarrow{b}|=\sqrt{{(\overrightarrow{a}+2\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{4+4×2×1×(-\frac{1}{2})+1}$=1…(5分)
(2)由(a+kb)⊥(2b-a),
得($\overrightarrow{a}$+k$\overrightarrow{b}$)•(2$\overrightarrow{b}$-$\overrightarrow{a}$)=0,即2k-4+(2-k)×2×1cos120°=0,
解得k=2…(10分)
点评 本题考查平面向量的数量积的运算,考查理解与运算能力,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,5,7} | B. | {3,7} | C. | {4,5,6} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{13}$ | B. | $\frac{9}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{11}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
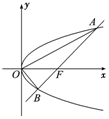 如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com