考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知条件导出B1C与面ABC所成的角∠B1CB=45°,AB⊥面B1BCC1,由此能证明面A1B1C⊥面B1BCC1.
(2)由已知条件推导出△AB1C为等边三角形,取B1C中点O,连结AO,BO,推导出∠AOB为二面角A-B1C-B的平面角,由此能求出二面角A-B1C-B的余弦值.
解答:
(1)证明:∵BB
1⊥面ABC
∴B
1C与面ABC所成的角为∠B
1CB
∴∠B
1CB=45°,∵BB
1=1,∴BC=1,
又∵BA=1,AC=
∴AB
2+BC
2=AC
2,∴AB⊥BC
∵BB
1⊥AB,BB
1∩BC=B,∴AB⊥面B
1BCC
1,
∵A
1B
1∥AB,∴A
1B
1⊥面B
1BCC
1,
∵A
1B
1?面A
1B
1C,∴面A
1B
1C⊥面B
1BCC
1.
(2)解:∵Rt△ABB
1中,BB
1=AB=1,∴AB
1=
,
∴△AB
1C为等边三角形,
又∵△BB
1C为等腰三角形,
∴取B
1C中点O,连结AO,BO,则AO⊥B
1C,BO⊥B
1C,
∴∠AOB为二面角A-B
1C-B的平面角,
∵在Rt△BB
1C中,BO=
,B
1C=
,
在等边△AB
1C中,AO=
,AC=
,
∴在△AOB中
cos∠AOB===.
∴二面角A-B
1C-B的余弦值为
.
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.

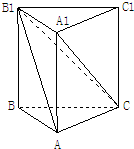
 如图,在直三棱柱ABC-A1B1C1中,AB=BB1=1,AC=
如图,在直三棱柱ABC-A1B1C1中,AB=BB1=1,AC= (2)解:∵Rt△ABB1中,BB1=AB=1,∴AB1=
(2)解:∵Rt△ABB1中,BB1=AB=1,∴AB1=
