
 ��ij�������и���������һ̨�磬�ݼ�⣬��ǰ̨������λ�ڳ���A������һ�㣩�Ķ�ƫ�ϦȽǷ���$��{cos��=\frac{{\sqrt{2}}}{10}}��$��300km�ĺ���P��������20km/h���ٶ�����ƫ��45�㷽���ƶ���̨����Ϯ�ķ�ΧΪԲ������ǰ�뾶Ϊ60km������10km/h���ٶȲ�������
��ij�������и���������һ̨�磬�ݼ�⣬��ǰ̨������λ�ڳ���A������һ�㣩�Ķ�ƫ�ϦȽǷ���$��{cos��=\frac{{\sqrt{2}}}{10}}��$��300km�ĺ���P��������20km/h���ٶ�����ƫ��45�㷽���ƶ���̨����Ϯ�ķ�ΧΪԲ������ǰ�뾶Ϊ60km������10km/h���ٶȲ����������� ��1������ֱ������ϵ������1�֣��������A��0��0������ǰ̨������$P��{30\sqrt{2}��-210\sqrt{2}}��$����tСʱ��̨������P������Ϊ��x��y���������⽨�������飬�����10Сʱ��̨�绹û�п�ʼ��Ϯ����A��
��2��tСʱ��̨����Ϯ�ķ�Χ����Ϊ��$P��{30\sqrt{2}-10\sqrt{2t}��-210\sqrt{2}+10\sqrt{2}t}��$ΪԲ�ģ�60+10tΪ�뾶��Բ���ɴ�����Բ����������������
��� 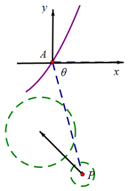 �⣺��1����ͼ����ֱ������ϵ������1�֣�
�⣺��1����ͼ����ֱ������ϵ������1�֣�
�����A��0��0������ǰ̨������$P��{30\sqrt{2}��-210\sqrt{2}}��$��
��tСʱ��̨������P������Ϊ��x��y����
��$\left\{\begin{array}{l}x=30\sqrt{2}-10\sqrt{2}t\\ y=-210\sqrt{2}+10\sqrt{2}t\end{array}\right.$����ʱ̨��İ뾶Ϊ60+10t��
10Сʱ��|PA|��184.4km��̨��İ뾶Ϊr=160km��
��r��|PA|������5�֣�
��10Сʱ��̨�绹û�п�ʼ��Ϯ����A������1�֣�
��2���ɣ�1��֪tСʱ��̨����Ϯ�ķ�Χ����Ϊ��$P��{30\sqrt{2}-10\sqrt{2t}��-210\sqrt{2}+10\sqrt{2}t}��$ΪԲ�ģ�60+10tΪ�뾶��Բ��
������A�ܵ�̨����Ϯ��
��$\sqrt{{{[{��{30\sqrt{2}-10\sqrt{2}t}��-0}]}^2}+{{[{��{-210\sqrt{2}+10\sqrt{2}t}��-0}]}^2}}�ܣ�{60+10t}��$��
��300t2-10800t+86400��0����t2-36t+288��0������5�֣�
���12��t��24����1�֣�
��ó�����̨����Ϯ�ij���ʱ��Ϊ12Сʱ������1�֣�
���� ���⿼��Բ�����������������е�ʵ��Ӧ�ã����е��⣬����ʱҪ�������⣬ע���ھ������е����������������ؽ������̣�


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��-2��1 �� | B�� | ��-3��2��-1�� | C�� | ��-3��-2��-1�� | D�� | ��-3��2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 336�� | B�� | 320�� | C�� | 192�� | D�� | 144�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �٢ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com