
分析 (1)由已知得△ABC重心M在以B、C为两个焦点的椭圆,由此能求出△ABC重心M的轨迹方程.
(2)利用代入法,即可求顶点A的轨迹方程.
解答 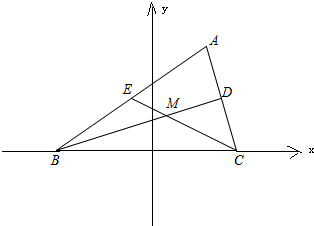 解:(1)如图所示,以线段BC所在直线为x轴、线段BC的中垂线为y轴建立直角坐标系…(2分)
解:(1)如图所示,以线段BC所在直线为x轴、线段BC的中垂线为y轴建立直角坐标系…(2分)
设M为△ABC的重心,BD是AC边上的中线,CE是AB边上的中线,由重心的性质知|BM|=$\frac{2}{3}$|BD|,|CM|=$\frac{2}{3}$|CE|,于是|MB|+|MC|=$\frac{2}{3}$|BD|+$\frac{2}{3}$|CE|=6…(4分)
根据椭圆的定义知,点M的轨迹是以B、C为焦点的椭圆.2a=6,2c=4,
∴a=3,b=$\sqrt{5}$,…(5分)
故所求的椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1(y≠0)…(6分)
(2)设A(x,y),则M($\frac{1}{3}$x,$\frac{1}{3}y$),代入$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1(y≠0),
可得出顶点A的轨迹方程为$\frac{{x}^{2}}{81}+\frac{{y}^{2}}{45}$=1(y≠0)…(12分)
点评 本题考查点的轨迹方程的求法,考查代入法,解题时要认真审题,注意椭圆定义的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $[\frac{e^2}{8},+∞)$ | B. | $(0,\frac{e^3}{27}]$ | C. | $[\frac{e^3}{27},+∞)$ | D. | $(0,\frac{e^2}{8}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a≥\frac{1}{8}$ | B. | $0<a≤\frac{1}{16}$ | C. | $-\frac{1}{8}≤a<0$ | D. | $-\frac{1}{2}<a≤\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数 | B. | 函数f(x)最小值为$\frac{3}{4}$ | ||
| C. | 函数f(x)在(0,$\frac{π}{2}$)内是减函数 | D. | $\frac{π}{2}$是函数f(x)的一个周期 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
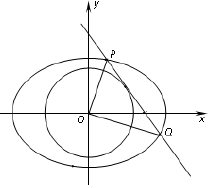 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,点(2,1)在椭圆C上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,点(2,1)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com