
 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)连接AB1,则∠B1C1A即为BC和AC1所成的角,由余弦定理,即可判断;
(2)连接AF,C1F,由正三棱柱的定义,即可判断;
(3)连接CD,则CD⊥AC1,且FD⊥AC1,则∠CDF为二面角F-AC1-C的平面角,通过解三角形CDF,即可判断;
(4)由于AD⊥平面CDF,通过VD-ACF=VA-DCF即可求出体积.
解答  解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2$\sqrt{2}$,
解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2$\sqrt{2}$,
AC1=2$\sqrt{2}$,cos∠B1C1A=$\frac{8+4-8}{2×2\sqrt{2}×2}$=$\frac{\sqrt{2}}{4}$,
故(1)错;
(2)连接AF,C1F,则易得AF=FC1=$\sqrt{5}$,
又FD⊥AC1,则AD=DC1,故(2)正确;
(3)连接CD,则CD⊥AC1,且FD⊥AC1,
则∠CDF为二面角F-AC1-C的平面角,CD=$\sqrt{2}$,CF=$\sqrt{5}$,DF=$\sqrt{3}$,
即CD2+DF2=CF2,故二面角F-AC1-C的大小为90°,面FAC1⊥面ACC1A1,故(3)正确;
(4)由于CD⊥AC1,且FD⊥AC1,则AD⊥平面CDF,
则VD-ACF=VA-DCF=$\frac{1}{3}$•AD•S△DCF=$\frac{1}{3}×\sqrt{2}×\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.故(4)正确.
故选:C.
点评 本题考查正三棱柱的定义和性质,考查线面垂直的判定和性质,空间的二面角,以及棱锥的体积,注意运用转换法,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )| A. | ①④ | B. | ①②③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
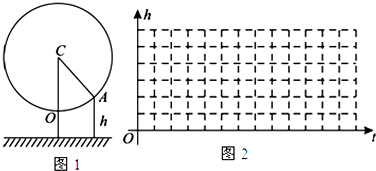
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
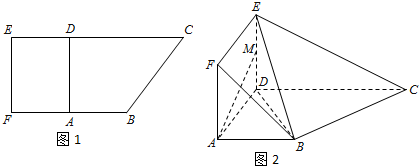
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.
如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 | 频率 | 关盘组占本组的比例 |
| 第一组 | [25,30) | 50 | 0.05 | 30% |
| 第二组 | [30,35) | 100 | 0.1 | 30% |
| 第三组 | [35,40) | 150 | 0.15 | 40% |
| 第四组 | [40,45) | 200 | 0.2 | 50% |
| 第五组 | [45,50) | a | b | 65% |
| 第六组 | [50,55) | 200 | 0.2 | 60% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com