Question

6．如图1，某大风车的半径为2米，每12秒沿逆时针方向匀速旋转一周，它的最低点O离地面1米．风车圆周上一点A从最低点O开始，运动t秒后与地面距离为h米．
（1）直接写出函数h=f（t）的关系式，并在给出的坐标系中用五点作图法作出h=f（t）在[0，12）上的图象（要列表，描点）；
（2）A从最低点O开始，沿逆时针方向旋转第一周内，有多长时间离地面的高度超过4米？

Answer 1

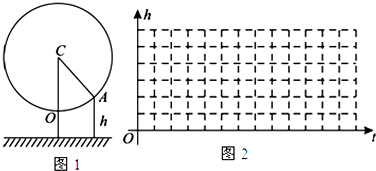
分析 （1）通过题意直接得h=f（t）=3-2$cos\frac{π}{6}t$，利用五点作图法即可；
（Ⅱ）通过3-2$cos\frac{π}{6}t$＞4，计算可得4＜t＜8．

解答 解：（1）h=f（t）=3-2$cos\frac{π}{6}t$，
列表：

$\frac{π}{6}t$	0	$\frac{π}{2}$	π	$\frac{3}{2}π$	2π
t	0	3	6	9	12
f（t）	3	1	5	1	3

描点连线：

（Ⅱ）∵3-2$cos\frac{π}{6}t$＞4，
∴$cos\frac{π}{6}t$＜-$\frac{1}{2}$，
又∵$\frac{2π}{3}$＜$\frac{π}{6}t$＜$\frac{4}{3}π$，t∈[0，12]，
∴4＜t＜8，
所以有4秒钟的时间离地面的高度超过4米．
注：用几何图形求解亦可．

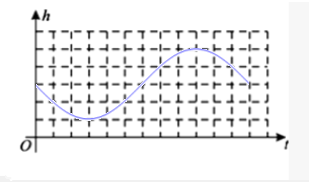
点评 本题考查三角函数在实际问题中的应用，考查五点作图法，注意解题方法的积累，属于中档题．