
分析 化简f(x)=(x2-2)?(2-x2)=$\left\{\begin{array}{l}{{x}^{2}-2,-\sqrt{2}≤x≤\sqrt{2}}\\{2-{x}^{2},x>\sqrt{2}或x<-\sqrt{2}}\end{array}\right.$,从而作函数f(x)与函数y=m的图象,结合图象可得.
解答 解:由题意,
f(x)=(x2-2)?(2-x2)
=$\left\{\begin{array}{l}{{x}^{2}-2,-\sqrt{2}≤x≤\sqrt{2}}\\{2-{x}^{2},x>\sqrt{2}或x<-\sqrt{2}}\end{array}\right.$,
作函数f(x)与函数y=m的图象如下,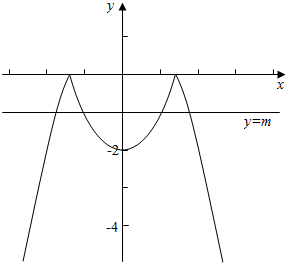
结合图象可得,
实数m的取值范围是(-2,0);
故答案为:(-2,0).
点评 本题考查了学生对新定义的接受与应用能力及数形结合的思想应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$) | C. | (0,$\frac{1}{2e}$) | D. | (0,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )| A. | ①④ | B. | ①②③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.
如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com