Question

20．已知Rt△ABC中，直角边AC、BC的长度分别为20、15，动点P从C出发，沿三角形边界按C→B→A方向移动；动点Q从C出发，沿三角形边界按C→A→B方向移动，移动到两点相遇时为止，且点Q移动的速度是点P移动的速度的2倍．设动点P移动的距离为x，△CPQ的面积为y，试求y与x之间的函数关系．

Answer 1

分析 根据点Q移动的速度是点P移动的速度的2倍，得到动点Q移动的距离为2x，根据点P，Q的位置，结合三角形的面积公式进行求解即可．

解答 解：∵Rt△ABC中，AC=20，BC=15，
∴AB=25，sinB=$\frac{4}{5}$，cosB=$\frac{3}{5}$，
∵点Q移动的速度是点P移动的速度的2倍，
∴设动点P移动的距离为x，则动点Q移动的距离为2x，
若两点相遇时，则满足x+2x=20+15+25，
即3x=60，即x=20．
①若Q在BC上，则0≤2x≤15，即0≤x≤$\frac{15}{2}$时，
△CPQ的面积为y=$\frac{1}{2}$•CQ•CP=$\frac{1}{2}•x•2x$=x²．
②若Q在AB上，P在CA上时，满足$\left\{\begin{array}{l}{15≤2x≤40}\\{0≤x≤20}\end{array}\right.$，即$\left\{\begin{array}{l}{\frac{15}{2}≤x≤20}\\{0≤x≤20}\end{array}\right.$．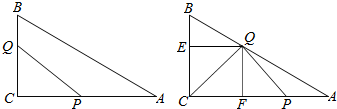
解得$\frac{15}{2}$≤x≤20，
则BQ=2x-BC=2x-15，BE=BQcosB=（2x-15）×$\frac{3}{5}$=$\frac{3（2x-15）}{5}$，
则三角形CPQ的高QF=EC=BC-BE=15-$\frac{3（2x-15）}{5}$=$\frac{120-6x}{5}$，
则△CPQ的面积为y=$\frac{1}{2}$•QF•CP=$\frac{1}{2}•x•$$\frac{120-6x}{5}$=$\frac{-3{x}^{2}+60x}{5}$，
即y=$\left\{\begin{array}{l}{{x}^{2}，}&{0≤x≤\frac{15}{2}}\\{\frac{-3{x}^{2}+60x}{5}，}&{\frac{15}{2}＜x≤20}\end{array}\right.$．

点评 本题主要考查函数的应用问题，根据条件结合点P，Q的位置关系，利用三角形的面积公式是解决本题的关键．