
已知双曲线C1与抛物线C2:y2=8x有相同的焦点F,它们在第一象限内的交点为M,若双曲线C1的焦距为实轴长的2倍,则|MF|=________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:填空题
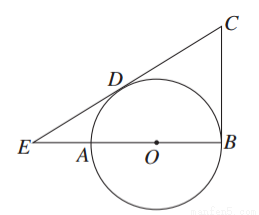
如图所示,AB是⊙O的直径,直线CB切⊙O于点B,直线CD切⊙O于点D,CD交BA的延长线于点E.若AB=3,ED=2,则BC的长为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:填空题
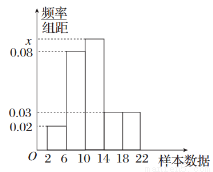
为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.某市抽取1000名年龄在[2,22](单位:岁)内的学生每天的零花钱,样本的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:选择题
某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:填空题
若C(-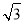 ,0),D(
,0),D(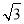 ,0),M是椭圆
,0),M是椭圆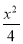 +y2=1上的动点,则
+y2=1上的动点,则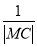 +
+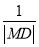 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:选择题
若双曲线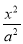 -
-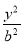 =1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
=1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
A.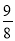 B.
B.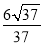 C.
C.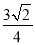 D.
D.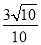
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:选择题
设A1,A2是椭圆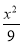 +
+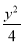 =1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
=1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
A.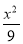 +
+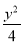 =1 B.
=1 B.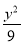 +
+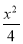 =1
=1
C.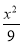 -
-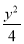 =1 D.
=1 D.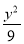 -
-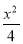 =1
=1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:解答题
已知顶点在坐标原点,焦点在x轴正半轴的抛物线上有一点A(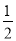 ,m),A点到抛物线焦点的距离为1.
,m),A点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设M(x0,y0)为抛物线上的一个定点,过M作抛物线的两条互相垂直的弦MP,MQ,求证:PQ恒过定点(x0+2,-y0).
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
已知椭圆C: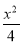 +
+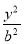 =1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
A.[1,4) B.[1,+∞)
C.[1,4)∪(4,+∞) D.(4,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com