Question

9．已知二次函数f（x）满足不等式f（x）＜5x-2的解集是（1，2），且f（x）的图象过点（-1，-1）．记函数g（x）=$\left\{\begin{array}{l}{|lo{g}_{2}x|，x＞0}\\{-f（x），x≤0}\end{array}\right.$．
（Ⅰ）求f（x）的解析式，并画出g（x）的图象；
（Ⅱ）求关于x的方程2g²（x）-5g（x）+2=0不同的根的个数．

Answer 1

分析 （Ⅰ）由已知可设f（x）=a（x-1）（x-2）+5x-2，且a＞0，将（-1，-1）代入可得f（x）的解析式，进而可得g（x）的解析式，画出g（x）的图象；
（Ⅱ）设t=g（x），则方程2g²（x）-5g（x）+2=0可化为：2t²-5t+2=0，结合（I）中图象，可得答案．

解答 解：（Ⅰ）∵f（x）＜5x-2的解集是（1，2），
故可设f（x）=a（x-1）（x-2）+5x-2，且a＞0，
又因为f（x）的图象过点（-1，-1），
所以a=1
所以f（x）=（x-1）（x-2）+5x-2=x²+2x．…（4分）
则g（x）=$\left\{\begin{array}{l}|lo{g}_{2}x|，x＞0\\-{x}^{2}-2x，x≤0\end{array}\right.$．其图象如下图所示：…（8分）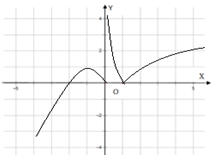

（Ⅱ）设t=g（x），则方程2g²（x）-5g（x）+2=0可化为：2t²-5t+2=0，
解得：t=$\frac{1}{2}$或t=2
即g（x）=$\frac{1}{2}$或g（x）=2，
由（I）图象可知方程g（x）=$\frac{1}{2}$有4个不同根，
方程g（x）=2有2个不同根．
从而所求方程共有6个不同的根．…（12分）

点评 本题考查的知识点是二次函数的图象和性质，分段函数的应用，数形结合思想，熟练掌握二次函数的图象和性质，是解答的关键．