
分析 由正弦函数的奇偶性即可判断则y=sin2x奇函数,故①错误; 由y=sin2x的最小正周期为T=$\frac{2π}{ω}$=π,故②正确;当x=0时,y=ln(x+1)=0,故函数存在零点,故③错误; 函数y=ln(x+1)在区间(-1,+∞)上单调递增,故函数y=ln(x+1)在区间(-1,0)上是增函数,④正确,即可求得答案.
解答 解:由正弦函数的性质可知:f(x)=y=sin2x,则f(-x)=sin(-2x)=-sin2x=-f(x),则y=sin2x奇函数,故①错误;
由y=sin2x的最小正周期为T=$\frac{2π}{ω}$=π,故②正确;
令函数y=ln(x+1)=0,即x+1=1,x=0,函数存在零点,故③错误;
由对数函数的单调性可知:函数y=ln(x+1)在区间(-1,+∞)上单调递增,
故函数y=ln(x+1)在区间(-1,0)上是增函数,④正确.
故答案为:②④
点评 本题考查正弦函数的性质,考查对数函数的单调性即零点存在定义,考查计算能力,属于基础题.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
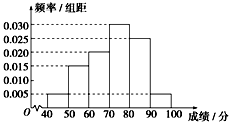 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com