
分析 由sinα-cosα=$\frac{1}{5}$,两边平方,再利用同角三角函数基本关系式、倍角公式,两角和与差的正弦函数公式即可得出.
解答 解:∵sinα-cosα=$\frac{1}{5}$,0≤2α≤2π,
∴两边平方可得:1-sin2α=$\frac{1}{25}$,可得:sin2α=$\frac{24}{25}$.
∵sinα-cosα=$\frac{1}{5}$>0,0≤α≤π,
∴sinα>cosα,$\frac{π}{4}$<α≤π,可得:$\frac{π}{2}$<2α≤2π,
又∵sin2α=$\frac{24}{25}$>0,可得:0<2α<π,从而可得:$\frac{π}{2}$<2α<π,
∴cos2α=-$\sqrt{1-si{n}^{2}2α}$=-$\frac{7}{25}$,
∴sin(2α-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$(sin2α-cos2α)=$\frac{\sqrt{2}}{2}$×($\frac{24}{25}$+$\frac{7}{25}$)=$\frac{31\sqrt{2}}{50}$.
故答案为:$\frac{24}{25}$,$\frac{31\sqrt{2}}{50}$.
点评 本题考查了同角三角函数基本关系式、倍角公式,两角和与差的正弦函数公式的应用,属于基础题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$<x1x2<$\frac{1}{e}$ | B. | $\frac{1}{e}$<x1x2<1 | C. | 1<x1x2<e | D. | x1x2>e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
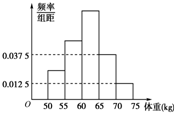 为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )
为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a,b,c恰成等差数列,若抽取的学生人数是48,则第2小组的频数为( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}[{1-{{({\frac{1}{3}})}^5}}]$ | B. | $\frac{1}{3}[{1-{{({\frac{1}{3}})}^5}}]$ | C. | $\frac{2}{3}[{1-{{({\frac{1}{2}})}^5}}]$ | D. | $\frac{3}{2}[{1-{{({\frac{1}{2}})}^5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com