练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a、b、c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4)>f(1)，则(　　)

    A．a>0,4a＋b＝0                                          B．a<0,4a＋b＝0

    C．a>0,2a＋b＝0                                          D．a<0,2a＋b＝0


    A

    [解析]　本题考查了二次函数的性质．

    由题意得f(0)＝c，f(4)＝16a＋4b＋c＝c，即16a＋4b＝0,4a＋b＝0，f(1)＝a＋b＋c，因为f(0)>f(1)，所以a＋b<0，a>0，故选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数f(x)＝loga(x2－ax＋5)(a>0且a≠1)满足对任意的x1、x2，当x1<x2≤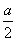时，f(x2)－f(x1)<0，则实数a的取值范围为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，既是偶函数又在(0，＋∞)单调递增的函数是(　　)

    A．y＝x3　　　　　　　　　                         B．y＝|x|＋1

    C．y＝－x2＋1                                              D．y＝2－|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合M是满足下列条件的函数f(x)的全体：(1)f(x)既不是奇函数也不是偶函数；

    (2)函数f(x)有零点．那么在函数①f(x)＝|x|－1，②f(x)＝2x－1，③f(x)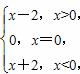＝④f(x)＝x2－x－1＋lnx中，属于M的有________．(写出所有符合条件的函数序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是定义在R上的奇函数，它的最小正周期为T，则f(－)的值为(　　)

    A．－                                                         B．0

    C.                                                             D．T

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝x2＋4x＋3在[－1,0]上的最大值是______，最小值是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝(cosx－a)2＋1，当cosx＝a时有最小值，当cosx＝－1时有最大值，则a的取值范围是(　　)

    A．[－1,0]　　　　　　                                B．[－1,1]

    C．(－∞，0]                                                D．[0,1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝a－|x|(a>0且a≠1)，若f(2)＝4，则f(－2)与f(1)的大小关系是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝log3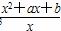，x∈(0，＋∞)，是否存在实数a，b，使f(x)同时满足下列条件：①在(0,1)上是减函数，在[1，＋∞)上是增函数；②f(x)的最小值是1.若存在，求出a，b的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案