
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() 的中点,过直线
的中点,过直线![]() ,
, ![]() 的平面分别与棱
的平面分别与棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,给出以下四个命题:
,给出以下四个命题:
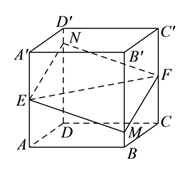
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
, ![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 是常函数;
是常函数;
④若多面体![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 为单调函数.
为单调函数.
其中假命题为( ).
A. ① B. ② C. ③ D. ④
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标平面中, ![]() 的两个顶点为
的两个顶点为![]() ,平面内两点
,平面内两点![]() 、
、![]() 同时满足:①
同时满足:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交弦分别为
相交弦分别为![]() ,设弦
,设弦![]() 的中点分别为
的中点分别为![]() .
.
①求四边形![]() 的面积
的面积![]() 的最小值;
的最小值;
②试问:直线![]() 是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租。该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() lnx-x+
lnx-x+![]() ,其中a>0.
,其中a>0.
(1)若f(x)在(0,+∞)上存在极值点,求a的取值范围;
(2)设a∈(1,e],当x1∈(0,1),x2∈(1,+∞)时,记f(x2)-f(x1)的最大值为M(a).那么M(a)是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() ,且点
,且点![]() 到椭圆C的两焦点的距离之和为
到椭圆C的两焦点的距离之和为![]() .
.

(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ) 若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与
与![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
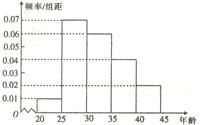
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
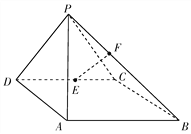
(Ⅰ)求证: ![]() ;
;
(Ⅱ)试确定点![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com