Question

14．给定函数f（x）和g（x），若存在实常数k，b，使得函数f（x）和g（x）对其公共定义域D上的任何实数x分别满足f（x）≥kx+b和g（x）≤kx+b，则称直线l：y=kx+b为函数f（x）和g（x）的“隔离直线”．给出下列四组函数：
①f（x）=$\frac{1}{2^x}$+1，g（x）=sinx；
②f（x）=x³，g（x）=-$\frac{1}{x}$；
③f（x）=x+$\frac{1}{x}$，g（x）=lgx；
④f（x）=2^x-$\frac{1}{2^x}，g（x）=\sqrt{x}$
其中函数f（x）和g（x）存在“隔离直线”的序号是①③．

Answer 1

分析 画出图象，数形结合即得答案．

解答 解：①f（x）=$\frac{1}{2^x}$+1与g（x）=sinx的公共定义域为R，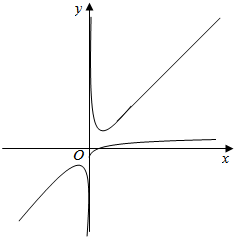
显然f（x）＞1，而g（x）≤1，故满足题意；
②f（x）=x³与g（x）=-$\frac{1}{x}$的公共定义域为：（-∞，0）∪（0，+∞），
当x∈（-∞，0）时，f（x）＜0＜g（x），
当x∈（0，+∞）时，g（x）＜0＜f（x），故不满足题意；
③f（x）=x+$\frac{1}{x}$与g（x）=lgx图象如右图，
显然满足题意；
④函数f（x）=2^x-$\frac{1}{2^x}，g（x）=\sqrt{x}$的图象如图，
显然不满足题意；
故答案为：①③．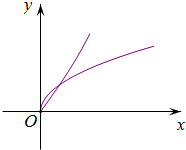

点评 本题主要考查函数的性质，数形结合是解题的关键，属于中档题．