
分析 (1)利用向量的运算法则和重心定理及数量积运算即可得出;
(2)利用向量的运算法则和内心性质及数量积运算即可得出.
解答 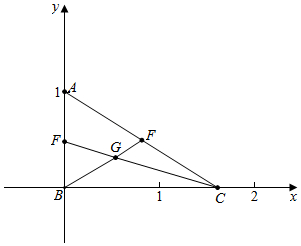 解:(1)以B为圆心,以BC所在直线为x轴,以BA所在的直线为y轴,建立如图所示的坐标系,
解:(1)以B为圆心,以BC所在直线为x轴,以BA所在的直线为y轴,建立如图所示的坐标系,
∵Rt△ABC中,|AB|=1,∠BAC=60°,∠B=90°,
∴|BC|=$\sqrt{3}$,|AC|=2
∴A(0,1),C($\sqrt{3}$,0),
设E、F分别为AC、AB的中点,
∴E($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),F(0,$\frac{1}{2}$),
∴$\overrightarrow{BE}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),$\overrightarrow{CF}$=(-$\sqrt{3}$,$\frac{1}{2}$),
∴$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{BE}$=($\frac{\sqrt{3}}{3}$,$\frac{1}{3}$),$\overrightarrow{CG}$=$\frac{2}{3}$$\overrightarrow{CF}$=(-$\frac{2\sqrt{3}}{3}$,$\frac{1}{3}$),
∴$\overrightarrow{GB}$•$\overrightarrow{GC}$=$\overrightarrow{BG}$•$\overrightarrow{CG}$=$\frac{\sqrt{3}}{3}$×(-$\frac{2\sqrt{3}}{3}$)+$\frac{1}{3}×\frac{1}{3}$=-$\frac{5}{9}$,
(2)∵G是△ABC的内心,
∴BE平分∠ABC,CF平分∠ACB,
∴∠GBC=45°,∠GCB=15°,
∴∠BGC=120°,
由正弦定理可得$\frac{BG}{sin15°}$=$\frac{CG}{sin45°}$=$\frac{BC}{sin120°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴BG=2sin15°=2sin(45°-30°)=$\frac{\sqrt{6}-\sqrt{2}}{2}$,CG=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
∴$\overrightarrow{GB}$•$\overrightarrow{GC}$=|$\overrightarrow{GB}$|•|$\overrightarrow{GC}$|cos120°=$\frac{\sqrt{6}-\sqrt{2}}{2}$×$\sqrt{2}$×(-$\frac{1}{2}$)=$\frac{1-\sqrt{3}}{2}$
点评 本题主要考查两个向量的数量积的定义,熟练掌握向量的运算法则和重心内心以及数量积运算、模的计算公式和及其两角和差的正弦弦公式是解题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$+π2 | B. | π+π2 | C. | $\frac{π}{2}$+$\frac{{π}^{2}}{2}$ | D. | π+$\frac{{π}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值-e | B. | 有最小值e | C. | 有最大值e | D. | 有最大值e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | ■ | 6.7 |
| A. | 4.8 | B. | 5.2 | C. | 5.8 | D. | 6.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com