
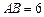 ,在线段
,在线段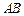 上任取两点C,D(端点
上任取两点C,D(端点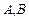 除外),将线段
除外),将线段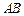 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
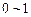 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是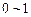 之间的均匀随机
之间的均匀随机 数)
数) ,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种.
,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种. ),共1种.
),共1种.
 , 所以所分成的三条线段可以构成三角形的概率为
, 所以所分成的三条线段可以构成三角形的概率为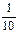 .
. 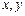 为分成三条线段中的两条长度.
为分成三条线段中的两条长度. 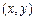 可以看成平面中的点,试验的全部结果所构成的区域为
可以看成平面中的点,试验的全部结果所构成的区域为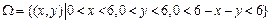 ,如图所示,其面积为
,如图所示,其面积为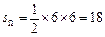 ,事件B所构成的区域为
,事件B所构成的区域为
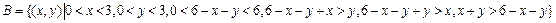 如图所示阴影部分,其面积为
如图所示阴影部分,其面积为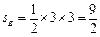 ,故
,故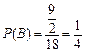

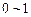 之间的均匀随机数X、Y(题目给出)
之间的均匀随机数X、Y(题目给出)
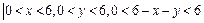 的点
的点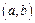 的个数N和落在
的个数N和落在
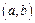 的个数N1,由已知中的20组随机数可数得N=13,N1=3
的个数N1,由已知中的20组随机数可数得N=13,N1=3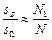 计算得:
计算得: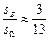 ,故
,故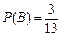


科目:高中数学 来源:不详 题型:解答题
 量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.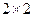 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系? ,
,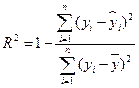 ,可能用到数据:
,可能用到数据: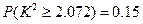 ,
,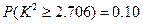 ,
,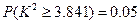 ,
,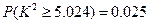 .)
.)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
 必过点( )
必过点( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
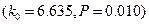
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
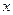 ,数学成绩为
,数学成绩为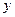 (注:没有相同姓名的学生).
(注:没有相同姓名的学生).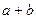 的值;
的值; 的概率;
的概率;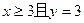 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |
 绩与班级有关系”。
绩与班级有关系”。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表| | 不及格 | 及格 | 总计 |
| 甲班 | 10 | 35 | M |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | N |
 观测值的计算式
观测值的计算式 =0.6527你有多大把握认为成绩及格与班级
=0.6527你有多大把握认为成绩及格与班级 有关?
有关? =7.121又说明什么?
=7.121又说明什么?
 )
) 0.100,P(k
0.100,P(k
 )
) 0.010)
0.010)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 /100kg)与上市时间
/100kg)与上市时间 (单位:天)的数据如下表:
(单位:天)的数据如下表:时间 | 50 | 110 |  250 250 |
| 种植成本Q | 150 | 108 | 150 |
 的变化关系的是 ( )
的变化关系的是 ( )A. | B.  |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com