
分析 若命题p为真:则$\left\{\begin{array}{l}{△>0}\\{-m<0}\\{1>0}\end{array}\right.$;若q:关于x的方程4x2+4(m一2)x+1=0没有实根,则△<0.若¬p或¬q为假.则¬(p∧q)为假,P∧A为真,即可得出.
解答 解:命题:p:关于x的方程x2+mx+1=0有两个不等的负根,则$\left\{\begin{array}{l}{△>0}\\{-m<0}\\{1>0}\end{array}\right.$,解得m>2;
q:关于x的方程4x2+4(m一2)x+1=0没有实根,∴△=16(m-2)2-16<0,解得1<m<3.
若¬p或¬q为假.则¬(p∧q)为假,
∴p∧q为真,
由p∧q为真可得:$\left\{\begin{array}{l}{m>2}\\{1<m<3}\end{array}\right.$,解得2<m<3.
∴实数m的取值范围是:(2,3).
点评 本题考查了复合命题真假的判定方法、一元二次的实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
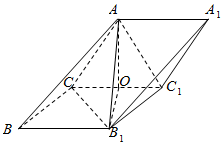 如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
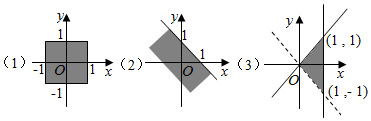
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | (-$\sqrt{3}$,-1)∪(1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y≥0}\\{x+2y≥3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y≥0}\\{x+2y≤3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-y≤0}\\{x+2y≥3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y≤0}\\{x+2y≤3}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 99 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com