
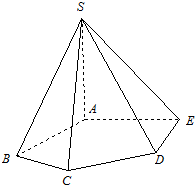
 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°分析 (Ⅰ)连结BE,由$BC=DE=\sqrt{3}$,得∠BCD=∠CDE=120°,推导出∠SBE 即为异面直线CD 与SB 所成的角.由此能求出异面直线CD 与SB 所成的角.
(Ⅱ)五边形ABCDE 是轴对称图形,从而BC⊥AB,再求出SA⊥BC,由此能证明BC⊥平面SAB.
(Ⅲ)作出二面角的平面角∠DFG,由此能求出二面角B-SC-D 的大小.
解答  解:(Ⅰ)连结BE,由$BC=DE=\sqrt{3}$,得∠BCD=∠CDE=120°,
解:(Ⅰ)连结BE,由$BC=DE=\sqrt{3}$,得∠BCD=∠CDE=120°,
由图形的对称性可知,四边形BCDE 是等腰梯形,BE∥CD,
∴∠SBE 即为异面直线CD 与SB 所成的角.
∵SA⊥平面ABCDE,SA=AB=AE=2,
∴SA⊥AB,SA⊥AE,$SB=SE=2\sqrt{2}$.
在△ABE 中,∵AB=AE=2,∠BAE=120°,∴$BE=2\sqrt{3}$.
在△SBE 中,∵$SB=SE=2\sqrt{2}$,$BE=2\sqrt{3}$,
∴$cos∠SBE=\frac{{\sqrt{3}}}{{2\sqrt{2}}}=\frac{{\sqrt{6}}}{4}$,$∠SBE=arccos\frac{{\sqrt{6}}}{4}$.
因此,异面直线CD 与SB 所成的角为$arccos\frac{{\sqrt{6}}}{4}$.
证明:(Ⅱ)由(Ⅰ)知,四边形BCDE 是等腰梯形,△ABE 是等腰三角形,
∴五边形ABCDE 是轴对称图形,
∴$∠ABC=∠AEC=\frac{1}{2}({540°}-{120°}-{120°}-{120°})={90°}$,即BC⊥AB.
又∵SA⊥平面ABCDE,∴SA⊥BC.
而SA∩AB=A,∴BC⊥平面SAB.
解:(Ⅲ)作出二面角的平面角∠DFG,
由题意知二面角B-SC-D 的大小为$π-arccos\frac{{7\sqrt{82}}}{82}$.
点评 本小题主要考查异面直线所成角、线面垂直、二面角等基础知识以及空间线面位置关系的证明、角和距离的计算,考查空间想象能力、逻辑推理能力和运算能力.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{14}}}{6}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
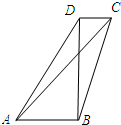 如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )
如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
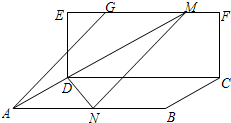 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com