
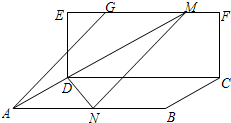
 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
分析 以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出二面角M-DN-C的平面角的取值范围.
解答 解: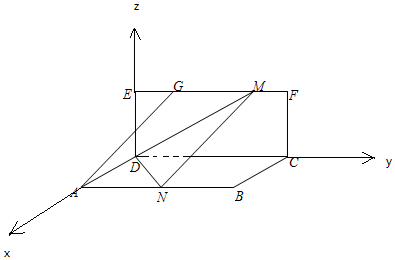 以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
∵AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,
EG=$\frac{1}{4}$EF=1,
点M在线段GF上(包括两端点),
点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,
∴0≤AN=EM≤3,
D(0,0,0),设N($\sqrt{2}$,a-1,0),a∈[1,4],则M(0,a,$\sqrt{3}$),
$\overrightarrow{DN}$=($\sqrt{2},a-1,0$),
$\overrightarrow{DM}$=(0,a,$\sqrt{3}$),
设平面DMN的法向量
$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DN}=\sqrt{2}x+(a-1)y=0}\\{\overrightarrow{n}•\overrightarrow{DM}=ay+\sqrt{3}z=0}\end{array}\right.$,取y=1,得$\overrightarrow{n}$=($\frac{a-1}{\sqrt{2}}$,1,-$\frac{a}{\sqrt{3}}$)
平面DNC的法向量$\overrightarrow{m}$=(0,0,1),
设二面角M-DN-C的平面角为θ,
则cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{2{a}^{2}}{5{a}^{2}-6a+9}$=$\frac{2}{9(\frac{1}{a}-\frac{1}{3})^{2}+4}$∈[$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$],
∴45°≤θ≤60°.
∴二面角M-DN-C的平面角的取值范围为[45°,60°].
故选:B.
点评 本题考查二面角的平面角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
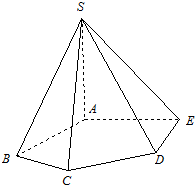 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 015. | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6356. | 7.879 | 10.828 |
| A. | 99.9% | B. | 99.5% | C. | 97.5% | D. | 95% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com