练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若关于x的不等式x2-ax-a-1≥0（x＞-1）恒成立，则实数a的取值范围是（-∞，-2]．

    分析 化简二次不等式可得（x+1）（x-（a+1））＞0，对a讨论，a=-2，a＞-2，a＜-2，求得解集，即可判断a的范围．

    解答 解：x2-ax-a-1≥0即为（x+1）（x-（a+1））＞0，
    当a=-2时，解集为{x|x∈R}，不等式在（-1，+∞）恒成立；
    当a＞-2时，解集为{x|x≥a+1或x≤-1}，不等式在（-1，+∞）不成立；
    当a＜-2时，解集为{x|x≥-1或x≤a+1}，不等式在（-1，+∞）恒成立．
    综上可得，a的范围是（-∞，-2]．
    故答案为：（-∞，-2]．

    点评 本题考查二次不等式的解法和不等式恒成立问题的解法，注意运用分类讨论的思想方法，考查运算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．焦点为（6，0）且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为（　　）
    A．$\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1B．$\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1C．$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1D．$\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设集介A={x|1＜（$\frac{1}{2}$）x＜8}，B={x|y=lg（x2+3x+2）}，从集合A中任取一个元素，则这个元素也是集合B中元素的概率是（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=x2-mx+1，对于任意x0∈R，存在y0＞0，使得f（x0）=y0，求m的范围：（-2，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．$\frac{1}{2sin10°}$-2sin70°的值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．己知a，b∈R，下列命题正确的是（　　）
    A．若a＞b，则$\frac{1}{a}$＞$\frac{1}{b}$B．若a＞b，则$\frac{1}{a}$＜$\frac{1}{b}$C．若|a|＞b，则a2＞b2D．若a＞|b|，则a2＞b2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知等差数列{an}满足：an+1＞an（n∈N*），a1=1，该数列的前三项分别加上1，1，3后成等比数列，an+2log2bn=-1．
    （Ⅰ）分别求数列{an}，{bn}的通项公式；
    （Ⅱ）求证：数列{an•bn}的前n项和Tn＜3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．下面四个图案，都是由小正三角形构成，设第n个图形中所有小正三角形边上黑点的总数为f（n）．

    （1）求出f（2），f（3），f（4），f（5）；
    （2）找出f（n）与f（n+1）的关系，并求出f（n）的表达式；
    （3）求证：$\frac{1}{f（1）}$+$\frac{1}{f（2）}$+$\frac{1}{f（3）}$+…+$\frac{1}{f（n）}$＜$\frac{2}{3}$（n∈N*）

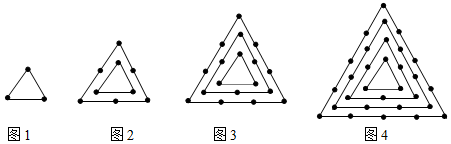
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知实数x、y满足条件$\left\{\begin{array}{l}{x≥2}\\{x+y≤4}\\{ax+y+5≥0}\end{array}\right.$，若目标函数z=3x+y的最小值为5，则a的值为（　　）
    A．-17B．-2C．2D．17

    查看答案和解析>>

    同步练习册答案