
【题目】已知函数![]() ,其图象相邻两条对称轴之间的距离为
,其图象相邻两条对称轴之间的距离为![]() ,将该函数的图象向左平移
,将该函数的图象向左平移![]() 个单位后,得到的图象对应的函数为偶函数.下列判断正确的是( )
个单位后,得到的图象对应的函数为偶函数.下列判断正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于点
的图象关于点![]() 对称
对称
C. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
D. 函数![]() 在
在![]() 上单调递增
上单调递增
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为20米,圆心角![]() 的扇形展示台,展示台分成了四个区域:三角形
的扇形展示台,展示台分成了四个区域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米
).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米![]() ,紫龙卧雪30元/米
,紫龙卧雪30元/米![]() ,朱砂红霜40元/米
,朱砂红霜40元/米![]() .
.
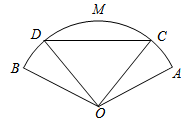
(1)设![]() ,试建立日效益总量
,试建立日效益总量![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试探求![]() 为何值时,日效益总量达到最大值.
为何值时,日效益总量达到最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断中正确的是( )
A.在![]() 中,“
中,“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() 成等差数列”
成等差数列”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.命题![]() :“
:“![]() ,使得
,使得![]() ”,则
”,则![]() 的否定:“
的否定:“![]() ,都有
,都有![]() ”
”
D.若平面内一动点到定点的距离等于它到定直线的距离,则该动点的轨迹是一条抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙、丙、丁四个人安排到座位号分别是![]() 的四个座位上,他们分别有以下要求,
的四个座位上,他们分别有以下要求,
甲:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一样;
丁:如果乙不坐座位号为![]() 的座位,我就不坐座位号为
的座位,我就不坐座位号为![]() 的座位.
的座位.
那么坐在座位号为![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若![]() ,
,![]() ,且
,且![]() ,则称
,则称![]() 调和分割
调和分割![]() .已知平面上的点
.已知平面上的点![]() 调和分割点
调和分割点![]() ,则下列说法正确的是
,则下列说法正确的是
A. ![]() 可能线段
可能线段![]() 的中点
的中点
B. ![]() 可能线段
可能线段![]() 的中点
的中点
C. ![]() 可能同时在线段
可能同时在线段![]() 上
上
D. ![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出直线![]() 与圆
与圆![]() 的交点极坐标及直线
的交点极坐标及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com