
分析 (Ⅰ)方法一、求出t=4时,椭圆方程和顶点A,设出直线AM的方程,代入椭圆方程,求交点M,运用弦长公式求得|AM|,由垂直的条件可得|AN|,再由|AM|=|AN|,解得k=1,运用三角形的面积公式可得△AMN的面积;
方法二、运用椭圆的对称性,可得直线AM的斜率为1,求得AM的方程代入椭圆方程,解方程可得M,N的坐标,运用三角形的面积公式计算即可得到;
(Ⅱ)直线AM的方程为y=k(x+$\sqrt{t}$),代入椭圆方程,求得交点M,可得|AM|,|AN|,再由2|AM|=|AN|,求得t,再由椭圆的性质可得t>3,解不等式即可得到所求范围.
解答 解:(Ⅰ)方法一、t=4时,椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,A(-2,0),
直线AM的方程为y=k(x+2),代入椭圆方程,整理可得(3+4k2)x2+16k2x+16k2-12=0,
解得x=-2或x=-$\frac{8{k}^{2}-6}{3+4{k}^{2}}$,则|AM|=$\sqrt{1+{k}^{2}}$•|2-$\frac{8{k}^{2}-6}{3+4{k}^{2}}$|=$\sqrt{1+{k}^{2}}$•$\frac{12}{3+4{k}^{2}}$,
由AN⊥AM,可得|AN|=$\sqrt{1+(-\frac{1}{k})^{2}}$•$\frac{12}{3+4•(\frac{-1}{k})^{2}}$=$\sqrt{1+{k}^{2}}$•$\frac{12}{3|k|+\frac{4}{|k|}}$,
由|AM|=|AN|,k>0,可得$\sqrt{1+{k}^{2}}$•$\frac{12}{3+4{k}^{2}}$=$\sqrt{1+{k}^{2}}$•$\frac{12}{3k+\frac{4}{k}}$,
整理可得(k-1)(4k2+k+4)=0,由4k2+k+4=0无实根,可得k=1,
即有△AMN的面积为$\frac{1}{2}$|AM|2=$\frac{1}{2}$($\sqrt{1+1}$•$\frac{12}{3+4}$)2=$\frac{144}{49}$;
方法二、由|AM|=|AN|,可得M,N关于x轴对称,
由MA⊥NA.可得直线AM的斜率为1,直线AM的方程为y=x+2,
代入椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,可得7x2+16x+4=0,
解得x=-2或-$\frac{2}{7}$,M(-$\frac{2}{7}$,$\frac{12}{7}$),N(-$\frac{2}{7}$,-$\frac{12}{7}$),
则△AMN的面积为$\frac{1}{2}$×$\frac{24}{7}$×(-$\frac{2}{7}$+2)=$\frac{144}{49}$;
(Ⅱ)直线AM的方程为y=k(x+$\sqrt{t}$),代入椭圆方程,
可得(3+tk2)x2+2t$\sqrt{t}$k2x+t2k2-3t=0,
解得x=-$\sqrt{t}$或x=-$\frac{t\sqrt{t}{k}^{2}-3\sqrt{t}}{3+t{k}^{2}}$,
即有|AM|=$\sqrt{1+{k}^{2}}$•|$\frac{t\sqrt{t}{k}^{2}-3\sqrt{t}}{3+t{k}^{2}}$-$\sqrt{t}$|=$\sqrt{1+{k}^{2}}$•$\frac{6\sqrt{t}}{3+t{k}^{2}}$,
|AN|═$\sqrt{1+\frac{1}{{k}^{2}}}$•$\frac{6\sqrt{t}}{3+\frac{t}{{k}^{2}}}$=$\sqrt{1+{k}^{2}}$•$\frac{6\sqrt{t}}{3k+\frac{t}{k}}$,
由2|AM|=|AN|,可得2$\sqrt{1+{k}^{2}}$•$\frac{6\sqrt{t}}{3+t{k}^{2}}$=$\sqrt{1+{k}^{2}}$•$\frac{6\sqrt{t}}{3k+\frac{t}{k}}$,
整理得t=$\frac{6{k}^{2}-3k}{{k}^{3}-2}$,
由椭圆的焦点在x轴上,则t>3,即有$\frac{6{k}^{2}-3k}{{k}^{3}-2}$>3,即有$\frac{({k}^{2}+1)(k-2)}{{k}^{3}-2}$<0,
可得$\root{3}{2}$<k<2,即k的取值范围是($\root{3}{2}$,2).
点评 本题考查椭圆的方程的运用,考查直线方程和椭圆方程联立,求交点,以及弦长公式的运用,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | m | C. | 2m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
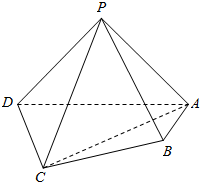 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com