
分析 (1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函数的最值,转化求解即可.
(2)求出g(x)=f(x)-2=ax+bx-2,求出函数的导数,构造函数h(x)=$(\frac{b}{a})^{x}$+$\frac{lna}{lnb}$,求出g(x)的最小值为:g(x0).同理①若g(x0)<0,g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,利用函数g(x)=f(x)-2有且只有1个零点,推出g(x0)=0,然后求解ab=1.
解答 解:函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)设a=2,b=$\frac{1}{2}$.
①方程f(x)=2;即:${2}^{x}+\frac{1}{{2}^{x}}$=2,可得x=0.
②不等式f(2x)≥mf(x)-6恒成立,即${2}^{2x}+\frac{1}{{2}^{2x}}$≥m(${2}^{x}+\frac{1}{{2}^{x}}$)-6恒成立.
令t=${2}^{x}+\frac{1}{{2}^{x}}$,t≥2.
不等式化为:t2-mt+4≥0在t≥2时,恒成立.可得:△≤0或$\left\{\begin{array}{l}{\frac{m}{2}≤2}\\{{2}^{2}-2m+4≥0}\end{array}\right.$
即:m2-16≤0或m≤4,
∴m∈(-∞,4].
实数m的最大值为:4.
(2)g(x)=f(x)-2=ax+bx-2,
g′(x)=axlna+bxlnb=ax[$\frac{lna}{lnb}$+$(\frac{b}{a})^{x}$]lnb,
0<a<1,b>1可得$\frac{b}{a}>1$,
令h(x)=$(\frac{b}{a})^{x}$+$\frac{lna}{lnb}$,则h(x)是递增函数,而,lna<0,lnb>0,
因此,x0=$lo{g}_{\frac{b}{a}}(-\frac{lna}{lnb})$时,h(x0)=0,
因此x∈(-∞,x0)时,h(x)<0,axlnb>0,则g′(x)<0.
x∈(x0,+∞)时,h(x)>0,axlnb>0,则g′(x)>0,
则g(x)在(-∞,x0)递减,(x0,+∞)递增,因此g(x)的最小值为:g(x0).
①若g(x0)<0,x<loga2时,ax>${a}^{lo{g}_{a}2}$=2,bx>0,则g(x)>0,
因此x1<loga2,且x1<x0时,g(x1)>0,因此g(x)在(x1,x0)有零点,
则g(x)至少有两个零点,与条件矛盾.
②若g(x0)>0,函数g(x)=f(x)-2有且只有1个零点,g(x)的最小值为g(x0),可得g(x0)=0,
由g(0)=a0+b0-2=0,
因此x0=0,因此$lo{g}_{\frac{b}{a}}(-\frac{lna}{lnb})$=0,-$\frac{lna}{lnb}$=1,即lna+lnb=0,ln(ab)=0,则ab=1.
可得ab=1.
点评 本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒成立的应用,考查分析问题解决问题的能力.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③⑤ | C. | ②③④ | D. | ①③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 9 | C. | 7 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
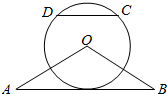 如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,$\frac{1}{2}$OA为半径作圆.
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,$\frac{1}{2}$OA为半径作圆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com