Question

在△ABC中，已知

AB

•

AC

=16，sinC=cosAsinB，S_△ABC=6，P为线段AC上的点，且

BP

=x

BA

| BA |

+y

BA

|BA|

，则xy的最大值为（　　）

• A、4
• B、3
• C、2
• D、1

Answer 1

考点：平面向量的基本定理及其意义,平面向量数量积的运算

专题：平面向量及应用

分析：在△ABC中，由sinC=cosAsinB，求得cosB=0，可得B=

π

2

．由

AB

•

AC

=16 求得|AB|=4，由S_△ABC=6，求得|BC|=3．
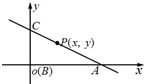
如图以B为原点，BA方向为x轴建立平面直角坐标系，由P为线段AC上的点可设

AP

=λ

AC

(0＜λ＜1)，即（x-4，y）=λ（-4，3），解得x=4-4λ，y=3λ，计算xy的值，并利用基本不等式求得它的最大值．

解答： 解：在△ABC中，∵sinC=cosAsinB，可得sinAcosB+cosAsinB=cosAsinB，
由sinA＞0得cosB=0，∴B=

π

2

．
由

AB

•

AC

=16 得|

AB

|2=16，∴|AB|=4，由S_△ABC=6，求得|BC|=3．
如图以B为原点，BA方向为x轴建立平面直角坐标系，由

BP

=x

BA

| BA |

+y

BC

| BC |

及向量坐标的定义，
可知P（x，y），A（4，0），B（0，3），
由P为线段AC上的点可设

AP

=λ

AC

(0＜λ＜1)，即（x-4，y）=λ（-4，3），
得：x=4-4λ，y=3λ，∴xy=3λ(4-4λ)=12λ(1-λ)≤12×(

λ+1-λ

2

)2=3．

点评：本题主要考查三角恒等变换，平面向量基本定理及其意义，两个向量坐标形式的运算，属于基础题．