
| A. | 若a1+a2<0,则a2+a3<0 | |
| B. | 若{an}是正数数列,a2+an-1=12,Sn=36.则a3a4的最小值为36 | |
| C. | 若a1<0,则(a2-a1)(a2-a3)>0 | |
| D. | 若0<a1<a2,则a2$>\sqrt{{a}_{1}{a}_{3}}$ |
分析 对于A,举例即可判断,
对于B,根据等差数列的性质和等差数列的前n项和公式,以及基本不等式即可判断,
对于C,根据等差数列的定义即可判断,
对于D,根据等差中项的性质和基本不等式即可判断.
解答 解:对于A,若a1=-2,a2=0,a3=2,满足a1+a2<0,但a2+a3>0,故A错误,
对于B,∵{an}是正数数列,a2+an-1=12,
∴a1+an=12,
∵Sn=36,
∴36=$\frac{12n}{2}$,n=6,
∴a1+a6=12,
∴a3+a4=12,
∴a3a4≤($\frac{{a}_{3}+{a}_{4}}{2}$)2=36,当且仅当a3=a4=6时等号成立,故B错误,
对于C,若a1<0,设公差为d,则(a2-a1)=d,(a2-a3)=-d,∴(a2-a1)(a2-a3)-d2<0,故C错误,
对于D,0<a1<a2,则2a2=a1+a3>2$\sqrt{{a}_{1}{a}_{3}}$,∴a2>$\sqrt{{a}_{1}{a}_{3}}$,故D正确,
故选:D.
点评 本题考查了等差数列的性质以及等差数列的前n项和公式,以及基本不等式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | e-l | B. | e | C. | 3 | D. | e+l |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
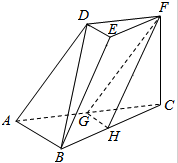 如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1] | B. | (1,2) | C. | (-3,0] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com