
分析 (Ⅰ)由已知得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,$\overrightarrow{PC}•\overrightarrow{PD}=(b-1)(-b-1)=-1,解得$b2=2,由此能求出椭圆E的方程.
(Ⅱ)(i)当直线l斜率不存在时,不存在这样的直线,当直线l斜率存在时,设方程为y=kx+1,与椭圆联立得(1+2k2)x2+4kx-2=0,由此利用韦达定理,能求出直线l的方程.
(ii)当直线l与x垂直时,$\frac{{\left|{QA}\right|}}{{\left|{QB}\right|}}=\frac{{\left|{PA}\right|}}{{\left|{PB}\right|}}$,对于任意直线l,欲证明$\frac{{\left|{QA}\right|}}{{\left|{QB}\right|}}=\frac{{\left|{PA}\right|}}{{\left|{PB}\right|}}$恒成立.只需证明:kQB+kQA=0.
解答 解:(Ⅰ)∵椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}\overrightarrow{•PD}=-1$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,∴a=$\sqrt{2}b=\sqrt{2}c$,
又C(0,b),D(0,-b),∴$\overrightarrow{PC}•\overrightarrow{PD}=(b-1)(-b-1)=-1,解得$b2=2,
∴a=2,∴椭圆E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(Ⅱ)(i)当直线l斜率不存在时,$\overrightarrow{PB}$=$\sqrt{2}-1$,$\overrightarrow{AP}$=$\sqrt{2}+1$,$\overrightarrow{PB}≠\frac{1}{2}\overrightarrow{AP}$,
不符合题意,不存在这样的直线,
当直线l斜率存在时,设方程为y=kx+1,A(x1,y1),B(x2,y2),
联立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+1}\end{array}\right.$,整理,得(1+2k2)x2+4kx-2=0,
由韦达定理得${x}_{1}+{x}_{2}=\frac{-4k}{1+2{k}^{2}}$,${x}_{1}{x}_{2}=\frac{-2}{1+2{k}^{2}}$,
由$\overrightarrow{PB}=\frac{1}{2}\overrightarrow{AP}$,得$({x}_{2},{y}_{2}-1)=\frac{1}{2}(-{x}_{1},1-{y}_{1})$,∴${x}_{2}=-\frac{1}{2}{x}_{1}$,
代入韦达定理,整理得${x}_{1}=\frac{-8k}{1+2{k}^{2}}$,${{x}_{1}}^{2}=\frac{4}{1+2{k}^{2}}$,
解得${k}^{2}=\frac{1}{14}$,∴k=$±\frac{\sqrt{14}}{14}$,
∴直线l的方程为$y=±\frac{\sqrt{14}}{14}x+1$.
证明:(ii)当直线l与x垂直时,$\frac{|QA|}{|QB|}=\frac{\sqrt{2}+1}{\sqrt{2}-1}=\frac{|PA|}{|PB|}$,∴命题成立.
下面证明对任意斜率存在的直线l,均有$\frac{|QA|}{|QB|}$=$\frac{|PA|}{|PB|}$,
即证:y轴为∠AQB的角平分线所在直线,只需证明:kQB+kQA=0
${k}_{QB}=\frac{{y}_{2}-2}{{x}_{2}}=\frac{k{x}_{2}-1}{{x}_{2}}$=$k-\frac{1}{{x}_{2}}$,${k}_{QA}=\frac{{y}_{1}-2}{{x}_{1}}$=$\frac{k{x}_{1}-1}{{x}_{1}}$=k-$\frac{1}{{x}_{1}}$,
∴${k}_{QB}+{k}_{QA}=2k-(\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}})$=2k-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,
由(1)中韦达定理得$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=2k,∴kQB+kQA=2k-2k=0,
∴对任意直线l,$\frac{|QA|}{|QB|}=\frac{|PA|}{|PB|}$恒成立.
点评 本题考查椭圆方程、直线方程的求法,考查两组线段比值相等的证明,是中档题,解题时要认真审题,注意等价转化思想的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
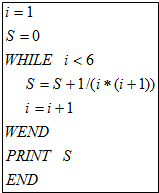
| A. | $\frac{53}{60}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,5] | B. | (2,5] | C. | [-1,2] | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -ln(e+1) | B. | -ln(4+e) | C. | -1 | D. | $-ln(e+\frac{1}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(α=2b>0),直线l过点A(2a,0),B(0,2b),原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(α=2b>0),直线l过点A(2a,0),B(0,2b),原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com