
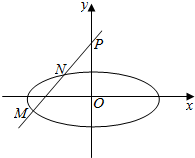
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(α=2b>0),直线l过点A(2a,0),B(0,2b),原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(α=2b>0),直线l过点A(2a,0),B(0,2b),原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$.分析 (1)由直线l过点A(2a,0),B(0,2b),可得直线l的方程为:$\frac{x}{2a}+\frac{y}{2b}$=1,化为bx+ay-2ab=0.原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$,可得$\frac{2ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{4\sqrt{5}}{5}$,又a=2b,联立解出即可.
(2)当直线l的斜率存在时,设直线l的方程为:y=kx+2,M(x1,y1),N(x2,y2).与椭圆方程联立化为:(1+4k2)x2+16kx+12=0,
△>0,化为:k2$>\frac{3}{4}$.假设存在λ>0使$\overrightarrow{QM}$=(λ+1)$\overrightarrow{QN}$-$λ\overrightarrow{QP}$成立(Q为直线l外的一点),化为:$\overrightarrow{OM}$=$(λ+1)\overrightarrow{ON}$-λ$\overrightarrow{OP}$,x1=x2(1+λ),与根与系数的关系联立可得.
解答 解:(1)∵直线l过点A(2a,0),B(0,2b),
∴直线l的方程为:$\frac{x}{2a}+\frac{y}{2b}$=1,化为bx+ay-2ab=0.
∵原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$,
∴$\frac{2ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{4\sqrt{5}}{5}$.
又a=2b,a2=b2+c2,
联立解得b=1,a=2,c=$\sqrt{3}$.
∴椭圆的方程为:$\frac{{x}^{2}}{4}$+y2=1.
(2)当直线l的斜率存在时,设直线l的方程为:y=kx+2,M(x1,y1),N(x2,y2).
联立:$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,化为:(1+4k2)x2+16kx+12=0,
△=(16k)2-48(1+4k2)>0,化为:k2$>\frac{3}{4}$.
∴x1+x2=$\frac{-16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$.(*)
假设存在λ>0使$\overrightarrow{QM}$=(λ+1)$\overrightarrow{QN}$-$λ\overrightarrow{QP}$成立(Q为直线l外的一点),
化为:$\overrightarrow{OM}$=$(λ+1)\overrightarrow{ON}$-λ$\overrightarrow{OP}$,
∴x1=x2(1+λ),与(*)联立可得:
0<$\frac{64(1+λ)}{(2+λ)^{2}}$=$\frac{3(1+4{k}^{2})}{{k}^{2}}$=$\frac{3}{{k}^{2}}$+12<16,λ>0.
解得:λ>0.
∴λ>0.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、直线的方程、点到直线的距离公式、向量坐标运算性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
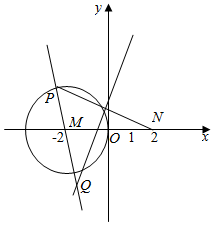 已知P为圆M:(x+2)2+y2=4上的动点,N(2,0),线段PN的垂直平分线与直线PM的交点为Q,点Q的轨迹方程为x2-$\frac{{y}^{2}}{3}$=1.
已知P为圆M:(x+2)2+y2=4上的动点,N(2,0),线段PN的垂直平分线与直线PM的交点为Q,点Q的轨迹方程为x2-$\frac{{y}^{2}}{3}$=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
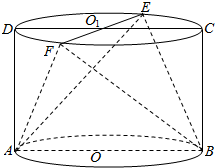 在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com