
分析 由题意可得,$x∈({0,\frac{1}{2}}]$时,函数y=2-2x的图象在函数y=logax的图象的下方,可得0<a<1.再根据它们的单调性可得$\frac{1}{2}$<loga$\frac{1}{2}$,解此对数不等式求得a的范围
解答 解:若对于任意的实数$x∈({0,\frac{1}{2}}]$,都有2-2x-logax<0恒成立,
即对于任意的实数$x∈({0,\frac{1}{2}}]$,都有logax>2-2x恒成立,
则y=logax的图象恒在y=${(\frac{1}{4})}^{x}$图象的上方,
∴0<a<1.
再根据它们的单调性可得$\frac{1}{2}$<loga$\frac{1}{2}$,
即$\sqrt{a}$>$\frac{1}{2}$,
∴a>$\frac{1}{4}$,
综上可得,$\frac{1}{4}$<a<1,
故答案为:$\frac{1}{4}$<a<1
点评 本题主要考查对数不等式的解法,同时考查对数函数的单调性,体现了转化的数学思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
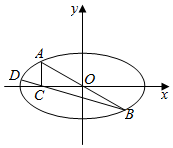 已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.
已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.
如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017 | B. | 4034 | C. | -4034 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},\frac{1}{3}})$ | B. | (-1,2) | C. | $({-\frac{4}{3},-\frac{1}{2}})$ | D. | (-2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com