
分析 设t=$\frac{ax-6}{x-2}$,利用复合函数单调性之间的关系进行求解即可.
解答 解:设t=g(x)=$\frac{ax-6}{x-2}$,则函数y=log${\;}_{\frac{1}{3}}$t为减函数,
∵f(x)=$lo{g}_{\frac{1}{3}}$$\frac{ax-6}{x-2}$(a为常数)在区间(3,5)上是减函数,
∴函数t=g(x)=$\frac{ax-6}{x-2}$在区间(3,5)上是增函数,且g(3)≥0
t=g(x)=$\frac{ax-6}{x-2}$=$\frac{a(x-2)+2a-6}{x-2}$=a+$\frac{2a-6}{x-2}$,
若t=g(x)=$\frac{ax-6}{x-2}$在区间(3,5)上是增函数,则2a-6<0,即a<3,
由g(3)≥0得g(3)=3a-6≥0,解得a≥2,
综上2≤a<3,
即实数a的取值范围是[2,3).
点评 本题主要考查函数单调性的应用,利用换元法结合对数函数和分数函数的单调性是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
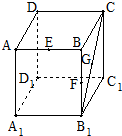 有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{47}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | [4,+∞) | C. | (-∞,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | $\frac{12}{25}$ | D. | -$\frac{12}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com