
分析 (1)求得函数的导数,令导数小于0,解二次不等式,注意x>0,可得单调减区间;
(2)由题意先求函数的定义域,再求导g′(x)=f′(x)-a=$\frac{1}{x}$-ax+1-a=$\frac{-a{x}^{2}+(1-a)x+1}{x}$,从而讨论导数的正负以确定函数的单调性.
(3)结合(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),构造函数,然后结合函数单调性得到要证的结论.
解答 解:(1)若a=2,则f(x)=lnx-x2+x,(x>0),
f′(x)=$\frac{1}{x}$-2x+1=-$\frac{(2x+1)(x-1)}{x}$,
f′(x)<0可得2x2-x-1>0,又x>0,解得x>1,
即有f(x)的减区间为(1,+∞),增区间为(0,1);
(2)f(x)≤ax-1恒成立,可得lnx-$\frac{1}{2}$ax2+x-ax+1≤0恒成立,
令g(x)=lnx-$\frac{1}{2}$ax2+x-ax+1,g′(x)═$\frac{-a{x}^{2}+(1-a)x+1}{x}$,
①当a≤0时,∵x>0,∴-ax2+(1-a)x+1>0,∴g′(x)>0
g(x)在(0,+∞)单调递增,且g(1)=-$\frac{3}{2}a+2>0$,
此时不等式f(x)≤ax-1不恒成立.
②当a>0时,g$′(x)=-\frac{a(x-\frac{1}{a})(x+1)}{x}$.
当$∈(0,\frac{1}{a}$)时,g′(x)>0,x$∈(\frac{1}{a},+∞)$时,g′(x)<0
∴g(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a},+∞$)d递减,
故g(x)max=g($\frac{1}{a}$)=$ln\frac{1}{a}-\frac{1}{2}a•(\frac{1}{a})^{2}+(1-a)•\frac{1}{a}+1=\frac{1}{2a}-lna$
令h(a)=$\frac{1}{2a}-lma$,(a>0),显然函数h(a)在(0,+∞)递减.
且h(1)=$\frac{1}{2}>0,h(2)=\frac{1}{2}-ln2<0$.
∴整数a的最小值为2.
(3)证明:由f(x1)+f(x2)+x1x2=0,
即lnx1+x12+x1+lnx2+x22+x2+x1x2=0,
从而(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),
令t=x1x2,则由φ(t)=t-lnt,
由x1>0,x2>0,即x1+x2>0.
φ′(t)=$\frac{t-1}{t}$.t>0
可知,φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.
所以φ(t)≥φ(1)=1,
所以(x1+x2)2+(x1+x2)≥1,解得:x1+x2≥$\frac{\sqrt{5}-1}{2}$.或x1+x$≤\frac{-\sqrt{5}-1}{2}$.
因为x1>0,x2>0,
因此x1+x2≥$\frac{\sqrt{5}-1}{2}$成立.
点评 本题考查导数的运用:求单调区间和极值、最值,主要考查不等式恒成立问题转化为求函数的最值问题,以及利用导数证明单调性进一步研究不等式问题的题型,注意运用参数分离和函数的零点存在定理,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
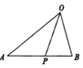 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{\sqrt{6}}}{3}π$ | B. | $\frac{{\sqrt{6}}}{2}π$ | C. | $\sqrt{6}π$ | D. | $3\sqrt{6}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com