
分析 根据f(x)的函数图象判断a,b,c的范围,利用f(a)=f(b)=f(c)得出a,b,c的关系,得出a+b+c关于a的函数,求出此函数的值域即可.
解答 解:作出函数f(x)的大致图象,如图所示: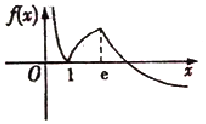
不妨设a<b<c,则0<a<1,1<b<e.
∵f(a)=f(b),即-lna=lnb,∴ab=1,即b=$\frac{1}{a}$,
同理-lna=2-lnc,∴$\frac{c}{a}$=e2,即c=ae2.
∴a+b+c=a+$\frac{1}{a}$+ae2=(e2+1)a+$\frac{1}{a}$,
又0<a<1,1<b<e,b=$\frac{1}{a}$,∴$\frac{1}{e}$<a<1,
令函数g(a)=(e2+1)a+$\frac{1}{a}$($\frac{1}{e}$<a<1),则g′(a)=e2+1-$\frac{1}{{a}^{2}}$>0,
∴g(a)在($\frac{1}{e}$,1)上单调递增,
∴g($\frac{1}{e}$)<g(a)<g(1),即2e+$\frac{1}{e}$<g(a)<e2+2.
∴2e+$\frac{1}{e}$<a+b+c<e2+2.
点评 本题考查了方程解与函数图象的关系,函数值域的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| ξ | -1 | 2 | 4 |
| P | $\frac{1}{5}$ | $\frac{2}{3}$ | p1 |
| A. | 0 | B. | $\frac{2}{15}$ | C. | $\frac{1}{15}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
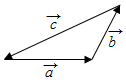
| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1296种 | B. | 216种 | C. | 864种 | D. | 1080种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 112 | B. | 278 | C. | 704 | D. | 1664 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com