
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由题意方程求得焦距,利用平面向量的减法运算得到$\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}}=\overrightarrow{{F}_{2}{F}_{1}}$,与已知|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=2$\sqrt{3}$同时两边平方后可得$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$,由此可得答案.
解答 解:如图,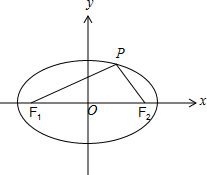
由椭圆$\frac{{x}^{2}}{4}$+y2=1,得a=2,b=1,c=$\sqrt{3}$,
$\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}}=\overrightarrow{{F}_{2}{F}_{1}}$,则$(\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}})^{2}={\overrightarrow{{F}_{2}{F}_{1}}}^{2}$,
即$|\overrightarrow{P{F}_{1}}{|}^{2}-2\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}+|\overrightarrow{P{F}_{2}}{|}^{2}=|\overrightarrow{{F}_{1}{F}_{2}}{|}^{2}$=12,
由|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=2$\sqrt{3}$,得$|\overrightarrow{P{F}_{1}}{|}^{2}+2\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}+|\overrightarrow{P{F}_{2}}{|}^{2}=12$,
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$,即$\overrightarrow{P{F}_{1}}⊥\overrightarrow{P{F}_{2}}$,
∴∠F1PF2=$\frac{π}{2}$.
故选:D.
点评 本题考查了椭圆的简单性质,考查了平面向量的数量积运算,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:解答题
已知函数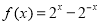 ,数列
,数列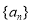 满足
满足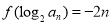 .
.
(1)求数列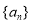 的通项公式;
的通项公式;
(2)证明:数列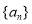 是递减数列.
是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是| A. | 存在n∈N,使得Sn+1=32$\sqrt{2}$a2b | B. | 存在n∈N,使得Sn+1=16$\sqrt{2}$a2b | ||
| C. | 对于任意n∈N,使得Sn+1≤32$\sqrt{2}$a2b | D. | 对于任意n∈N,使得Sn+1≥16$\sqrt{2}$a2b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com