
分析 (Ⅰ)函数f(x)的定义域为(0,+∞).当a=-2时,${f}^{'}(x)=2x-\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,由此利用导数性质能求出函数f(x)的单调区间和极值.
(Ⅱ) 由g(x)=x2+alnx+$\frac{2}{x}$,得${g}^{'}(x)=2x+\frac{a}{x}-\frac{2}{{x}^{2}}$,令φ(x)=$\frac{2}{x}-2{x}^{2}$,则φ′(x)=-$\frac{2}{{x}^{2}}-4x$.由此利用导数性质能求出a的取值范围.
解答 解:(Ⅰ)∵函数f(x)=x2+alnx,∴函数f(x)的定义域为(0,+∞).
当a=-2时,${f}^{'}(x)=2x-\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$.
当x变化时,f′(x)和f(x)的值的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
点评 本题考查函数的单调区间和极值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意构造法和导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P={-3,0,1} | B. | Q={-1,0,1,2} | C. | R={y|-π<y<-1,y∈Z} | D. | S={x||x|≤$\sqrt{3}$,x∈N} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
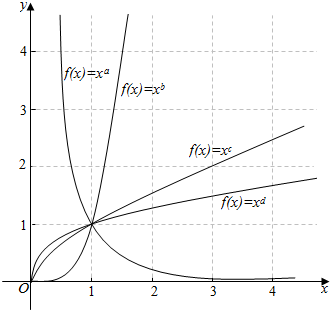
| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
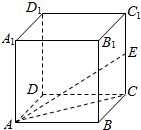
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com