
分析 (Ⅰ)将a的值带入f(x),两边平方求出不等式的解集即可;
(Ⅱ)求出f(x)=|x-a|-|x|+$\frac{a}{2}$,原问题等价于|a|<a2,求出a的范围即可.
解答 解:(Ⅰ)a=3时,f(x)=|x-3|-$\frac{1}{2}$x<0,
即|x-3|<$\frac{1}{2}$x,
两边平方得:(x-3)2<$\frac{1}{4}$x2,
解得:2<x<6,
故不等式的解集是{x|2<x<6};
(Ⅱ)f(x)-f(x+a)
=|x-a|-$\frac{1}{2}$x-|x|+$\frac{1}{2}$(x+a)
=|x-a|-|x|+$\frac{a}{2}$,
若对于任意的实数x,不等式f(x)-f(x+a)<a2+$\frac{a}{2}$恒成立,
即|x-a|-|x|+$\frac{a}{2}$<a2+$\frac{a}{2}$对x∈R恒成立,
即a2>|x-a|-|x|,而|x-a|-|x|≤|(x-a)-x|=|a|,
原问题等价于|a|<a2,又a>0,
∴a<a2,解得a>1.
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
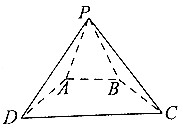 已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.
已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
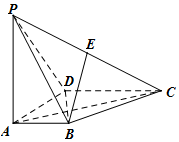 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com