
分析 求出原函数的导函数,得到f′($\frac{1}{2}$)=2,然后由直线方程的点斜式得曲线在点($\frac{1}{2}$,f($\frac{1}{2}$))处的切线方程.
解答 解:由题意,f′(x)=$\frac{1}{{x}^{2}}$-$\frac{1}{x}$
∴f′($\frac{1}{2}$)=2,
即曲线在点x=$\frac{1}{2}$处的切线的斜率为2.
∵f($\frac{1}{2}$)=-1+ln2
∴曲线在点($\frac{1}{2}$,f($\frac{1}{2}$))处的切线方程为y+1-ln2=2×(x-$\frac{1}{2}$),
整理得:2x-y-2+ln2=0.
点评 本题考查利用导数研究曲线上某点处的切线方程,曲线在某点处的切线的斜率,就是函数在该点处的导数值,是基础题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:选择题
函数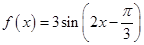 的图象为
的图象为 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.函数 关于直线
关于直线 对称
对称
B.图像 关于点
关于点 对称
对称
C. 在区间
在区间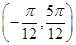 上递增
上递增
D.由 的图象向右平移
的图象向右平移 个单位长度可得
个单位长度可得
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
在 中,角
中,角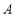 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 满足
满足 ,
, ,
,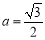 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com