
| A. | (1+x)2n | B. | (1-x)n | C. | (1-x2)n | D. | 2n+1 |
分析 由题意可得,(1+x)n =${C}_{n}^{0}$+${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2+${C}_{n}^{3}$•x3+…+${C}_{n}^{n}$•xn=A+B,且(1-x)n =${C}_{n}^{0}$-${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2-${C}_{n}^{3}$•x3+…+(-1)n•${C}_{n}^{n}$•xn=A-B,从而求得A2-B2 的值.
解答 解:由题意可得,(1+x)n =${C}_{n}^{0}$+${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2+${C}_{n}^{3}$•x3+…+${C}_{n}^{n}$•xn=A+B,
(1-x)n =${C}_{n}^{0}$-${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2-${C}_{n}^{3}$•x3+…+(-1)n•${C}_{n}^{n}$•xn=A-B,
∴A2-B2=(1-x2)n,
故选:C.
点评 本题主要考查二项式定理的应用,明白二项式的结构巧妙赋值是解答本题的关键属于基础题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
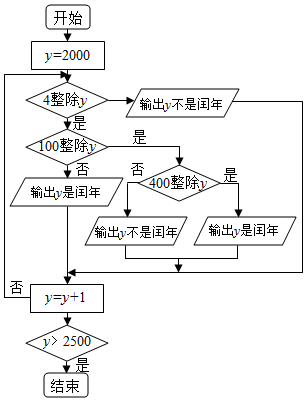
| A. | 输出年份y∈[2000,2500)且y∈N“哪年是闰年”“哪年不是闰年” | |
| B. | 输出年份y∈[2000,2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C. | 输出年份y∈[2000,2500)且y∈N“多少年是闰年”“多少年不是闰年” | |
| D. | 输出年份y∈[2000,2500]且y∈N“多少年是闰年”“多少年不是闰年” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com