
分析 通过计算出前几项的值猜想并用数学归纳法证明an=2n-1,进而通过计算出数列{M(an)}前几项的值可知从第2项起数列{M(an)}是以4为周期的周期数列,进而可得结论.
解答 解:依题意,${{a}_{2}}^{2}$=a1a2+$2{{a}_{1}}^{2}$,
即${{a}_{2}}^{2}$=a2+2,解得:a2=2或a2=-1(舍),
$2{{a}_{3}}^{2}$=3a2a3+$2{{a}_{2}}^{2}$,即$2{{a}_{3}}^{2}$=6a3+8,
解得:a3=4或a3=-1(舍),
$3{{a}_{4}}^{2}$=5a3a4+$2{{a}_{3}}^{2}$,即$3{{a}_{4}}^{2}$=20a4+32,
解得:a4=8或a4=-$\frac{4}{3}$(舍),
$4{{a}_{5}}^{2}$=7a4a5+$2{{a}_{4}}^{2}$,即$4{{a}_{5}}^{2}$=56a5+128,
解得:a5=16或a5=-2(舍),
猜想:an=2n-1.
下面用数学归纳法来证明:
①当n=1时,显然成立;
②假设当n=k(k≥2)时,有ak=2k-1,
∵kak+12=(2k-1)ak+1ak+2ak2,
∴kak+12-(k•2k-2k-1)ak+1-22k-1=0,
解得:ak+1=2k,或ak+1=-$\frac{{2}^{k-1}}{k}$(舍),
即当n=k+1时命题成立;
由①、②可知an=2n-1.
∴M(a1)=M(1)=1,
M(a2)=M(2)=2,
M(a3)=M(22)=4,
M(a4)=M(23)=8,
M(a5)=M(24)=6,
M(a6)=M(25)=2,
∴从第2项起数列{M(an)}是以4为周期的周期数列,
∴M(a2017)=M(22016)=6,
故答案为:6.
点评 本题考查数列的通项,考查数学归纳法,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{7}}}{7}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 21007 | D. | 21008 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
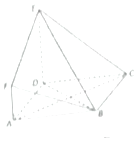 如图所示,四边形ABCD为菱形,AF=2,AF∥DE,DE⊥平面ABCD.
如图所示,四边形ABCD为菱形,AF=2,AF∥DE,DE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4032}{2017}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com