练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知等差数列{an}的前n项和为Sn，若a3，a5是方程x2-8x+15=0的两根，则S7=28．

    分析 由韦达定理及等差数列通项公式得a3+a5=2a4=8，从而a4=4，由此利用等差数列前n项和公式能示出S7．

    解答 解：∵a3，a5是方程x2-8x+15=0的两根，
    ∴a3+a5=2a4=8，
    解得a4=4，
    ∴S7=$\frac{7}{2}（{a}_{1}+{a}_{7}）$=7a4=28．
    故答案为：28．

    点评 本题考查等差数列的前7项和的求法，是基础题，解题时要认真审题，注意韦达定理和等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知平面直角坐标系xOy中，以O为极点，x轴的非负半轴为极轴建立极坐标系，P点的极坐标为（3，$\frac{π}{4}$）．曲线C的参数方程为ρ=2cos（θ-$\frac{π}{4}$）（θ为参数）．
    （Ⅰ）写出点P的直角坐标及曲线C的直角坐标方程；
    （Ⅱ）若Q为曲线C上的动点，求PQ的中点M到直线l：2ρcosθ+4ρsinθ=$\sqrt{2}$的距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知各项均为正数的等比数列{an}中，2a7+a8=a9．数列{bn}满足bn=log2an，且其前10项为45，则数列{an}的通项公式为an=2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．由函数y=lnx和y=ex-1的图象与直线x=1所围成的封闭图形的面积是e-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．定义运算$|{\begin{array}{l}{a}&b\\{c}&d\end{array}}|$=ad-bc，若z=$|{\begin{array}{l}{1}&2\\{i}&{i^2}\end{array}}|$，则复数$\overline z$对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．若不等式x-10＞0或x+2＜0成立时，不等式x-m＞1或x+m＜1（m＞0）不恒成立，且若不等式x-m＞1或x+m＜1（m＞0）成立时，不等式x一10＞0或x+2＜0成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{{e}^{2x}-1}{x}$．
    （1）求函数f（x）的单调区间；
    （2）若任意x∈（0，1），f（x）∈（a，b）恒成立，求b-a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

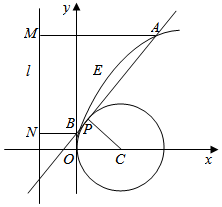
    1．在“2016”的logo设计中，有这样一个图案，其由线段l、抛物线弧E及圆C三部分组成，对其进行代数化的分析，如图建系，发现：圆C方程为（x-4）2+y2=16，抛物线弧E：y2=2px（y≥0，0≤x≤8），若圆心C恰为抛物线y2=2px的焦点，线段l所在的直线恰为抛物线y2=2px的准线．
    （Ⅰ）求p的值及线段l所在的直线方程；
    （Ⅱ）P为圆C上的任意一点，过P作圆的切线交抛物线弧E于A、B两点，问是否存在这样的点P，使得弦AB在l上的投影长度与圆C的直径之比为4：3？若存在，求出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

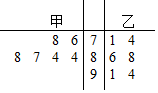    2．甲，乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示，则关于甲，乙两同学的成绩分析正确的是（　　）
    A．甲，乙两同学测试成绩的中位数相同
    B．甲，乙两同学测试成绩的众数相同
    C．甲，乙两同学测试成绩的平均数不相同
    D．甲同学测试成绩的标准差比乙同学测试成绩的标准差大

    查看答案和解析>>

    同步练习册答案