
分析 a=0时,不等式不可能恒成立;a≠0,若对任意的x>0时均有(ax-1)•[x2-(a+1)x-1]≥0,则函数y1=ax-1,y2=x2-(a+1)x-1,与x轴交于同一点,代入可得答案.
解答 解:(1)a=0时,代入题中不等式明显不恒成立.
(2)a≠0,构造函数y1=ax-1,y2=x2-(a+1)x-1,它们都过定点P(0,-1),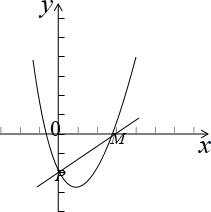
考查函数y1=ax-1:
令y=0,得M($\frac{1}{a}$,0),
∴a>0;
考查函数y2=x2-(a+1)x-1,
∵x>0时均有(ax-1)[x2-(a+1)x-1]≥0,
∴y2=x2-(a+1)x-1过点M($\frac{1}{a}$,0),
代入得:($\frac{1}{a}$)2-(a+1)•$\frac{1}{a}$-1=0,
解之得:a=$\frac{1}{2}$,或a=-1(舍去).
故答案为:$\frac{1}{2}$.
点评 本题考查的知识点为函数恒成立问题,函数的图象和性质,分类讨论思想,数形结合思想,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 直线 | C. | 线段 | D. | 一条射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com